Entrei agora em funções logarítmas, mas me deparei aqui com a prova do professor e tens umas coisas q eu nunca vi.
"e" eu vi na internete q é uma tal de constante de Euler
Mas ele colocou aqui numa lista para resolver um tal de "ln" q eu ainda não entendi
![a) ln*{e}^{\sqrt[]{2}}
b)2*ln(x)=1
c) ln(5 - 2x) = -3 a) ln*{e}^{\sqrt[]{2}}
b)2*ln(x)=1
c) ln(5 - 2x) = -3](/latexrender/pictures/326b86e809cb4b01fca61fcb170c2d78.png)
SE alguém puder me ajudar eu agradeço!


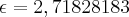

 então
então  , não é essa a ideia? hehehehhe
, não é essa a ideia? hehehehhe
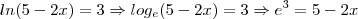
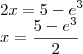
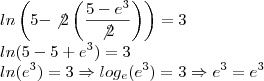
![\sqrt[]{\epsilon} = \epsilon^{\frac{1}{2}} \sqrt[]{\epsilon} = \epsilon^{\frac{1}{2}}](/latexrender/pictures/3bf31ae298649bc753b84c0a83d3308a.png)
![2^{\frac{2}{3}} = \sqrt[3]{2^2} 2^{\frac{2}{3}} = \sqrt[3]{2^2}](/latexrender/pictures/224ed6efa316441648e8c2e7a1a6f1e3.png)
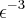
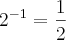
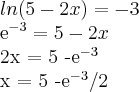

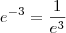 então:
então: 
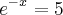
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.