 por jamiel » Ter Jun 14, 2011 15:45
por jamiel » Ter Jun 14, 2011 15:45
Olá!
Entrei agora em funções logarítmas, mas me deparei aqui com a prova do professor e tens umas coisas q eu nunca vi.
"
e" eu vi na internete q é uma tal de constante de Euler
Mas ele colocou aqui numa lista para resolver um tal de "ln" q eu ainda não entendi
![a) ln*{e}^{\sqrt[]{2}}
b)2*ln(x)=1
c) ln(5 - 2x) = -3 a) ln*{e}^{\sqrt[]{2}}
b)2*ln(x)=1
c) ln(5 - 2x) = -3](/latexrender/pictures/326b86e809cb4b01fca61fcb170c2d78.png)
SE alguém puder me ajudar eu agradeço!
-
jamiel
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Jan 31, 2011 15:48
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Mecânica
- Andamento: cursando
 por Claudin » Ter Jun 14, 2011 16:01
por Claudin » Ter Jun 14, 2011 16:01
O "e" seria como você disse a constante de Euller que equivale a
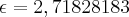
O "ln" seria nada mais que o Logaritmo Natural ou Logaritmo Neperiano
Que é o logaritmo na base "e", aqui nesse link você vai obter mais informações sobre o assunto
http://pt.wikipedia.org/wiki/Logaritmo_naturaltente resolver e qualquer coisa volte com dúvidas.
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por jamiel » Ter Jun 14, 2011 16:15
por jamiel » Ter Jun 14, 2011 16:15
Blza!
Então, b) seria ln(x)=1/2?
e ln(5-2x)=-3 --> ln(-3) = 5-2*(-3) ---> ln(-3)=11
?
-
jamiel
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Jan 31, 2011 15:48
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Mecânica
- Andamento: cursando
 por carlosalesouza » Ter Jun 14, 2011 17:24
por carlosalesouza » Ter Jun 14, 2011 17:24
Levando a resolução até o fim, meu caro...
Se 2.ln(x) = 1, vc está certo, ln(x) = 1/2... isso quer dizer que

No outro item, veja bem... façamos sempre essa mesma relação quando usamos logaritmos:
se

então

, não é essa a ideia? hehehehhe
Assim, como disse meu camarada, claudin, o logaritmo natural é o logaritmo de base

O que isso quer dizer? que:
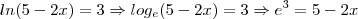
A partir daqui resolvemos a equação:
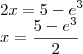
Ok?
Quer a prova? tudo bem... heheheheh
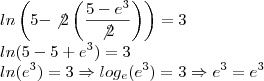
hehehehhe
Um abraço
Carlos Alexandre
Ciências Contábeis - FECEA/PR
Matemática - UEPG/PR
-
carlosalesouza
- Colaborador Voluntário

-
- Mensagens: 103
- Registrado em: Sex Abr 29, 2011 17:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática -LIC
- Andamento: cursando
 por jamiel » Ter Jun 14, 2011 17:46
por jamiel » Ter Jun 14, 2011 17:46
Thanks!
Deixa v se eu entendi ...!
Agora, tem uma coisa q aí q eu não estou lembrando, deve ser algum propriedade de potência q não me vem a cabeça deste momento:
Tipo: ?e ---> e^(1/2) qual seria a diferença entre os dois?
é menos três --->
log e (5-2x) = "-3"
Eu q é pq eu não estou abituado a esse "ln"
-
jamiel
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Jan 31, 2011 15:48
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Mecânica
- Andamento: cursando
 por Claudin » Ter Jun 14, 2011 17:51
por Claudin » Ter Jun 14, 2011 17:51
![\sqrt[]{\epsilon} = \epsilon^{\frac{1}{2}} \sqrt[]{\epsilon} = \epsilon^{\frac{1}{2}}](/latexrender/pictures/3bf31ae298649bc753b84c0a83d3308a.png)
Não existe diferença, pois eles são equivalentes.
É uma propriedade de potência --->
![2^{\frac{2}{3}} = \sqrt[3]{2^2} 2^{\frac{2}{3}} = \sqrt[3]{2^2}](/latexrender/pictures/224ed6efa316441648e8c2e7a1a6f1e3.png)
E o -3 que você mencionou ai é só substituir
o que vai ficar
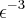
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Claudin » Ter Jun 14, 2011 17:53
por Claudin » Ter Jun 14, 2011 17:53
Vale lembrar mais uma propriedade de potência em que
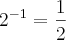
Abraço
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por jamiel » Ter Jun 14, 2011 19:14
por jamiel » Ter Jun 14, 2011 19:14
Seria assim:
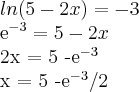
?
-
jamiel
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Jan 31, 2011 15:48
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Mecânica
- Andamento: cursando
 por carlosalesouza » Ter Jun 14, 2011 19:47
por carlosalesouza » Ter Jun 14, 2011 19:47
Pois é... eu não reparei no sinal de menos...
Quando posto durante a tarde, estou no Colégio, onde trabalho... o monitor é horripilante... hkkkkk
Enfim...
mudando o sinal da resposta que eu apresentei vai ficar:

Como
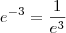
então:

Fazendo a substituição no logaritmo, encontraremos novamente a prova real da resposta...
Um grande abraço
Carlos Alexandre
Ciências Contábeis - FECEA/PR
Matemática - UEPG/PR
-
carlosalesouza
- Colaborador Voluntário

-
- Mensagens: 103
- Registrado em: Sex Abr 29, 2011 17:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática -LIC
- Andamento: cursando
 por jamiel » Ter Jun 14, 2011 21:04
por jamiel » Ter Jun 14, 2011 21:04
thanks!
Tem algumas coisas q eu só consigo fazer por tentativa!
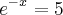
5/e = 1,8
e/5 = 1,5
1,8 - 1,5 = 1,3
x está entre 1,3 e 1,8
x = 1,6
e^(-1,6) = 5
1/(e^(1,6) = 5
1/e^(1,6) = 1/2 = 5
-
jamiel
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Jan 31, 2011 15:48
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Mecânica
- Andamento: cursando
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- DÚVIDA URGENTE!!
por tatahsooares » Seg Dez 13, 2010 01:32
- 0 Respostas
- 1395 Exibições
- Última mensagem por tatahsooares

Seg Dez 13, 2010 01:32
Matemática Financeira
-
- Dúvida urgente
por deborakisses » Dom Mai 08, 2011 16:05
- 1 Respostas
- 1418 Exibições
- Última mensagem por Molina

Dom Mai 08, 2011 18:19
Geometria Espacial
-
- Duvida URGENTE
 por legendkiller2009 » Qua Jun 01, 2011 19:18
por legendkiller2009 » Qua Jun 01, 2011 19:18
- 3 Respostas
- 2214 Exibições
- Última mensagem por carlosalesouza

Qui Jun 02, 2011 18:35
Cálculo: Limites, Derivadas e Integrais
-
- Duvida Urgente!
por RJCT » Qua Jun 13, 2012 18:50
- 1 Respostas
- 1479 Exibições
- Última mensagem por LuizAquino

Sex Jun 15, 2012 16:52
Cálculo: Limites, Derivadas e Integrais
-
- Duvida [Urgente] - Otimização
por Asustek27 » Qui Mai 27, 2010 11:26
- 3 Respostas
- 2095 Exibições
- Última mensagem por MarceloFantini

Sex Mai 28, 2010 08:41
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![a) ln*{e}^{\sqrt[]{2}}
b)2*ln(x)=1
c) ln(5 - 2x) = -3 a) ln*{e}^{\sqrt[]{2}}
b)2*ln(x)=1
c) ln(5 - 2x) = -3](/latexrender/pictures/326b86e809cb4b01fca61fcb170c2d78.png)


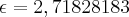

 então
então  , não é essa a ideia? hehehehhe
, não é essa a ideia? hehehehhe
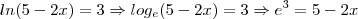
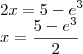
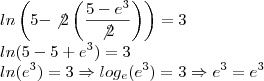
![\sqrt[]{\epsilon} = \epsilon^{\frac{1}{2}} \sqrt[]{\epsilon} = \epsilon^{\frac{1}{2}}](/latexrender/pictures/3bf31ae298649bc753b84c0a83d3308a.png)
![2^{\frac{2}{3}} = \sqrt[3]{2^2} 2^{\frac{2}{3}} = \sqrt[3]{2^2}](/latexrender/pictures/224ed6efa316441648e8c2e7a1a6f1e3.png)
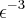
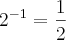
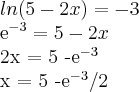

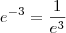 então:
então: 
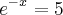


 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.