 por gustavoluiss » Qua Jun 01, 2011 22:30
por gustavoluiss » Qua Jun 01, 2011 22:30
É uma questão de vestibular gostaria que fosse respondida para continuar nos meus estudos,pois não entendi nada ou quase nada.
(Fuvest) Uma partícula desloca-se em um plano Oxy de modo que sua abscissa x e sua ordenada y são dadas pelas seguintes equações horárias:
x = 3t + 1 e y = 4t + 2, onde x e y são dadas em metros e t em segundos.
a) Qual o módulo da velocidade?
b) Qual a equação da trajetória?
c) Qual a forma da trajetória?
Resp:
A) 5 m/s
B) y= (4/3)X + 2/3 ; com x maior ou igual a 2.
C) Retilínea
-
gustavoluiss
- Colaborador Voluntário

-
- Mensagens: 118
- Registrado em: Ter Nov 23, 2010 15:59
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por Molina » Qua Jun 01, 2011 23:17
por Molina » Qua Jun 01, 2011 23:17
Boa noite, Gustavo!
gustavoluiss escreveu:a) Qual o módulo da velocidade?
Faça t = 0 e t = 1 (por exemplo) e faça a distância entre estes pontos.
gustavoluiss escreveu:b) Qual a equação da trajetória?
Multiplique a equação de x por 4 e a equação de y por 3 e subtraia elas.
gustavoluiss escreveu:c) Qual a forma da trajetória?
Equação de primeiro grau é uma reta.

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por gustavoluiss » Qui Jun 02, 2011 10:47
por gustavoluiss » Qui Jun 02, 2011 10:47
Okay,poderia te explicado melhor .
-
gustavoluiss
- Colaborador Voluntário

-
- Mensagens: 118
- Registrado em: Ter Nov 23, 2010 15:59
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por Molina » Sex Jun 03, 2011 07:57
por Molina » Sex Jun 03, 2011 07:57
gustavoluiss escreveu:Okay,poderia te explicado melhor .
Ficou alguma dúvida em algum item?
Eu poderia resolver todo o problema para você, mas pensar um pouco faz bem.
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por gustavoluiss » Sex Jun 03, 2011 14:00
por gustavoluiss » Sex Jun 03, 2011 14:00
Eu intendi a primeira vc fez a distancia e boto no intervalo de 1 segundo, né tá certo,mais a segunda porque a equação da trajetoria vai ser dada por aquela equação ?
E a c é fácil pensar também,obrigado pode explicar a segunda ficarei grato.
-
gustavoluiss
- Colaborador Voluntário

-
- Mensagens: 118
- Registrado em: Ter Nov 23, 2010 15:59
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por Molina » Sex Jun 03, 2011 14:12
por Molina » Sex Jun 03, 2011 14:12
Boa tarde.
gustavoluiss escreveu:Eu intendi a primeira vc fez a distancia e boto no intervalo de 1 segundo, né tá certo,mais a segunda porque a equação da trajetoria vai ser dada por aquela equação ?
E a c é fácil pensar também,obrigado pode explicar a segunda ficarei grato.
Temos duas equações, x e y, tais que ambas em função de t.
Podemos transformar em apenas umas equação, tentando eliminar o t.
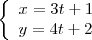
Porém, para eliminar o t neste sistema, podemos usar o artifício de deixas os coeficientes iguais e posteriormente diminui uma equação pela outra. Mas para deixar os coeficientes de t iguais, precisamos multiplicar a primeira equação toda por 4 e a segunda equação toda por 3 (para obter 12t):
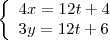
Agora fazendo a subtração da primeira equação pela segunda, termo a termo, obtemos:
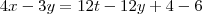
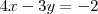
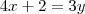
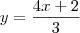

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por gustavoluiss » Sex Jun 03, 2011 21:02
por gustavoluiss » Sex Jun 03, 2011 21:02
Obrigado,
-
gustavoluiss
- Colaborador Voluntário

-
- Mensagens: 118
- Registrado em: Ter Nov 23, 2010 15:59
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por Ericka » Qui Jan 05, 2012 20:17
por Ericka » Qui Jan 05, 2012 20:17
Tive dúvida na mesma questão, mas continuo sem entender porque (na letra A) a distância entre 2 pontos vai definir a velocidade da partícula.
Agradeço desde já
-
Ericka
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qui Jan 05, 2012 20:04
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Arkanus Darondra » Qui Jan 05, 2012 20:32
por Arkanus Darondra » Qui Jan 05, 2012 20:32
Ericka escreveu:Tive dúvida na mesma questão, mas continuo sem entender porque (na letra A) a distância entre 2 pontos vai definir a velocidade da partícula.
A distância entre 2 pontos mostra o espaço percorrido.
Como
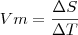
e
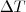
vale 1 basta encontrar a distância entre os 2 pontos.
-
Arkanus Darondra
- Colaborador Voluntário

-
- Mensagens: 187
- Registrado em: Seg Dez 26, 2011 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Ericka » Sex Jan 06, 2012 14:17
por Ericka » Sex Jan 06, 2012 14:17
Obrigado!
-
Ericka
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qui Jan 05, 2012 20:04
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Questão da Fuvest
por Kelvin Brayan » Qua Mar 02, 2011 11:56
- 2 Respostas
- 4133 Exibições
- Última mensagem por Kelvin Brayan

Qua Mar 02, 2011 13:23
Álgebra Elementar
-
- Questão Fuvest
 por Alex Rom » Qua Mar 30, 2011 11:38
por Alex Rom » Qua Mar 30, 2011 11:38
- 2 Respostas
- 3622 Exibições
- Última mensagem por Alex Rom

Qua Mar 30, 2011 12:07
Geometria Plana
-
- Questão da Fuvest
por my2009 » Qua Mar 30, 2011 10:00
- 4 Respostas
- 3018 Exibições
- Última mensagem por FilipeCaceres

Qua Mar 30, 2011 11:18
Estatística
-
- Questão da Fuvest
 por Kelvin Brayan » Seg Abr 18, 2011 17:11
por Kelvin Brayan » Seg Abr 18, 2011 17:11
- 2 Respostas
- 1724 Exibições
- Última mensagem por Kelvin Brayan

Ter Abr 19, 2011 12:57
Álgebra Elementar
-
- Questão FUVEST
por Guilherme Carvalho » Ter Mai 10, 2011 17:19
- 5 Respostas
- 2882 Exibições
- Última mensagem por carlosalesouza

Sex Mai 13, 2011 15:50
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




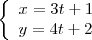
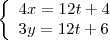
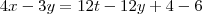
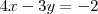
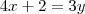
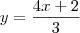

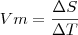 e
e 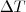 vale 1 basta encontrar a distância entre os 2 pontos.
vale 1 basta encontrar a distância entre os 2 pontos.![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.