 por maria cleide » Dom Mai 29, 2011 17:35
por maria cleide » Dom Mai 29, 2011 17:35
O maior valor inteiro que verifica a inequação

é:
A( )-negativo
B( )-primo
C( )-ímpar maior que 4
D( )-par positivo
Desenvolvendo:
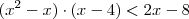

Mas agora não sei como continuar.
-
maria cleide
- Usuário Parceiro

-
- Mensagens: 54
- Registrado em: Dom Mai 08, 2011 12:57
- Formação Escolar: ENSINO FUNDAMENTAL I
- Andamento: cursando
 por Claudin » Dom Mai 29, 2011 21:37
por Claudin » Dom Mai 29, 2011 21:37
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por LuizAquino » Dom Mai 29, 2011 22:01
por LuizAquino » Dom Mai 29, 2011 22:01
Não se trabalha com inequações como se fossem equações. Principalmente quando é necessário dividir ou multiplicar toda a inequação por uma expressão.
O correto é seguir os passos:
x(x - 1)(x - 4) < 2(x - 4)
x(x - 1)(x - 4) - 2(x - 4) < 0
[x(x - 1) - 2](x - 4) < 0
(x² - x - 2)(x - 4) < 0
Agora, você deve analisar o sinal de cada um dos fatores para concluir o exercício.
SugestãoPara terminar de resolver o exercício, eu recomendo que você assista as vídeo-aulas sobre inequações no canal do Nerckie:
http://www.youtube.com/nerckieLeia o tópico:
inequação, dúvida.viewtopic.php?f=106&t=3856
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por maria cleide » Ter Mai 31, 2011 22:41
por maria cleide » Ter Mai 31, 2011 22:41
A partir daí fiz assim:
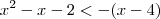
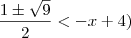
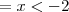
ou
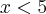
Està certa a minha resolução?
-
maria cleide
- Usuário Parceiro

-
- Mensagens: 54
- Registrado em: Dom Mai 08, 2011 12:57
- Formação Escolar: ENSINO FUNDAMENTAL I
- Andamento: cursando
 por LuizAquino » Qua Jun 01, 2011 00:41
por LuizAquino » Qua Jun 01, 2011 00:41
A sua resolução está errada.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por carlosalesouza » Qua Jun 01, 2011 00:48
por carlosalesouza » Qua Jun 01, 2011 00:48
Não está certa, não... absolutamente...
note que os parênteses estão se multiplicando... vc passou para o outro lado como se estivessem se somando...
O que vc deve fazer agora é encontrar as raízes de cada polinômio que está entre parênteses...
No caso, temos um polinômio de 1º e um de 2º grau... serão 3 raízes... depois disso, vc monta dois seguimentos de reta e verifica o sinal que f(x) terá em cada intervalo e depois encontra o produto dos sinais (negativo e positivo), para encontrar os intervalos desejados... neste caso, o maior valor inteiro em que o produto seja menor que zero...
deu pra entender? ficou complicado?
Se estiver com dificuldade, sigo com a recomendação do nosso magnânimo Luiz Aquino... acesso o canal do Nerckie... é bem mastigado, fácil de aprender...
QUalquer coisa, continua postando que a gente continua ajudando em tudo o que for possível...
Um abraço
Carlos Alexandre
Ciências Contábeis - FECEA/PR
Matemática - UEPG/PR
-
carlosalesouza
- Colaborador Voluntário

-
- Mensagens: 103
- Registrado em: Sex Abr 29, 2011 17:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática -LIC
- Andamento: cursando
 por maria cleide » Qui Jun 02, 2011 22:20
por maria cleide » Qui Jun 02, 2011 22:20
Como assim três raízes?
Na aula do Nerkie não consegui ver isso não.
Resolve um polinômio de cada vez.Será assim:
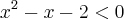
ou igual a zaro?
E depois como resolve o outro?
-
maria cleide
- Usuário Parceiro

-
- Mensagens: 54
- Registrado em: Dom Mai 08, 2011 12:57
- Formação Escolar: ENSINO FUNDAMENTAL I
- Andamento: cursando
 por LuizAquino » Qui Jun 02, 2011 22:29
por LuizAquino » Qui Jun 02, 2011 22:29
Esse tipo de inequação é chamada de "inequação produto". A partir da
vídeo-aula "Matemática - Aula 9 - Inequações - Parte 5" há a explicação sobre esse tipo de inequação. Eu recomendo que você assista essas vídeo-aulas.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por maria cleide » Dom Jun 05, 2011 18:25
por maria cleide » Dom Jun 05, 2011 18:25
Assisti a aula e encontrei a resposta, deu 3.
Obrigada
-
maria cleide
- Usuário Parceiro

-
- Mensagens: 54
- Registrado em: Dom Mai 08, 2011 12:57
- Formação Escolar: ENSINO FUNDAMENTAL I
- Andamento: cursando
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Maior valor
por thadeu » Qua Nov 25, 2009 16:17
- 4 Respostas
- 2945 Exibições
- Última mensagem por LuizAquino

Qua Mar 09, 2011 22:14
Álgebra Elementar
-
- Questão prova concurso (maior valor de y)
por fernandocez » Dom Mar 06, 2011 12:34
- 6 Respostas
- 3009 Exibições
- Última mensagem por LuizAquino

Dom Mar 06, 2011 17:10
Geometria Analítica
-
- Qual é o menor e o maior valor de x na expressão
por andersontricordiano » Seg Out 03, 2011 16:56
- 1 Respostas
- 3941 Exibições
- Última mensagem por MarceloFantini

Seg Out 03, 2011 21:10
Trigonometria
-
- Valor de x na inequação
por chenz » Qua Jul 21, 2010 21:45
- 1 Respostas
- 1410 Exibições
- Última mensagem por Tom

Qui Jul 22, 2010 01:38
Funções
-
- Inequação - Achar o valor de M
 por rafaleans » Sex Mar 14, 2014 09:21
por rafaleans » Sex Mar 14, 2014 09:21
- 0 Respostas
- 1099 Exibições
- Última mensagem por rafaleans

Sex Mar 14, 2014 09:21
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 é:
é: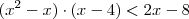


 é:
é: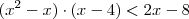


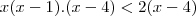
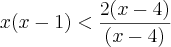
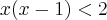


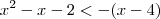
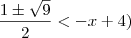
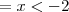 ou
ou 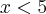



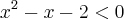 ou igual a zaro?
ou igual a zaro?



 .
.



