 por carlosalesouza » Qua Jun 01, 2011 00:48
por carlosalesouza » Qua Jun 01, 2011 00:48
Não está certa, não... absolutamente...
note que os parênteses estão se multiplicando... vc passou para o outro lado como se estivessem se somando...
O que vc deve fazer agora é encontrar as raízes de cada polinômio que está entre parênteses...
No caso, temos um polinômio de 1º e um de 2º grau... serão 3 raízes... depois disso, vc monta dois seguimentos de reta e verifica o sinal que f(x) terá em cada intervalo e depois encontra o produto dos sinais (negativo e positivo), para encontrar os intervalos desejados... neste caso, o maior valor inteiro em que o produto seja menor que zero...
deu pra entender? ficou complicado?
Se estiver com dificuldade, sigo com a recomendação do nosso magnânimo Luiz Aquino... acesso o canal do Nerckie... é bem mastigado, fácil de aprender...
QUalquer coisa, continua postando que a gente continua ajudando em tudo o que for possível...
Um abraço
Carlos Alexandre
Ciências Contábeis - FECEA/PR
Matemática - UEPG/PR
 é:
é: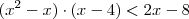


 é:
é: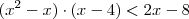


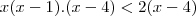
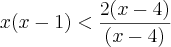
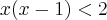


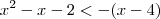
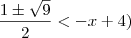
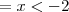 ou
ou 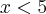



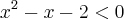 ou igual a zaro?
ou igual a zaro?


![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)