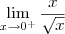por Claudin » Qua Mai 18, 2011 21:19
por Claudin » Qua Mai 18, 2011 21:19
![\lim_{x\rightarrow0}\frac{x}{\sqrt[]{x}} \lim_{x\rightarrow0}\frac{x}{\sqrt[]{x}}](/latexrender/pictures/41d1c6f9cac6aa6e7731c6f6e1f48d03.png)
![\lim_{x\rightarrow0}\frac{x}{\sqrt[]{x}} . \frac{\sqrt[]{x}}{\sqrt[]{x}} \lim_{x\rightarrow0}\frac{x}{\sqrt[]{x}} . \frac{\sqrt[]{x}}{\sqrt[]{x}}](/latexrender/pictures/f39052e533faf1d814aff069e6616660.png)
![\lim_{x\rightarrow0}\frac{x.\sqrt[]{x}}{x} = \frac{\sqrt[]{x}}{0} = 0 \lim_{x\rightarrow0}\frac{x.\sqrt[]{x}}{x} = \frac{\sqrt[]{x}}{0} = 0](/latexrender/pictures/5e4c7fbb8e2ec20882e9e4b1738ceee0.png)
A resolução do exercicio acima esta correta? se a resolução final fosse
![\frac{0}{\sqrt[]{x}} \frac{0}{\sqrt[]{x}}](/latexrender/pictures/529f52e095fc9ce86bacfefa3040d087.png)
a resposta seria

ou

? E se fosse
![\frac{1}{\sqrt[]{x}} \frac{1}{\sqrt[]{x}}](/latexrender/pictures/911233eacfdf6c16c12ac8d1e3dc6824.png)
qual seria a resposta final?
Obrigado
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por MarceloFantini » Qua Mai 18, 2011 21:26
por MarceloFantini » Qua Mai 18, 2011 21:26
Claudin, está nítido que você não está sabendo percebe o que está fazendo. Vamos lá:
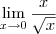
. Vamos trabalhar como potências:

Note que na sua resolução você surgiu (?) com um zero no denominador e manteve a raíz no numerador, e isso "daria infinito", porém deu zero. É

a variável, é ela que tende a zero.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Claudin » Qua Mai 18, 2011 21:30
por Claudin » Qua Mai 18, 2011 21:30
![\frac{x.\sqrt[]{x}}{x} = \frac{\sqrt[]{x}}{1} \frac{x.\sqrt[]{x}}{x} = \frac{\sqrt[]{x}}{1}](/latexrender/pictures/d64719a654b11a507a6bd41534b143dd.png)
a resposta seria essa entao?
eu cortei x com x
pois estava multiplicando meu erro so foi em vez de colocar 1 coloquei 0
Nao foi so isso nao?
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por MarceloFantini » Qua Mai 18, 2011 21:40
por MarceloFantini » Qua Mai 18, 2011 21:40
Foi, foi isso sim. Mas dava a entender erros piores. É bom perceber que foi apenas digitação.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Claudin » Qua Mai 18, 2011 21:44
por Claudin » Qua Mai 18, 2011 21:44
Obrigado pela ajuda Marcelo
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por LuizAquino » Qui Mai 19, 2011 10:58
por LuizAquino » Qui Mai 19, 2011 10:58
Claudin, você tem certeza que esse é o limite que apareceu como exercício?
Esse limite, do jeito que está, não existe nos reais. Isso porque para x aproximando-se de 0 pela esquerda (ou seja, x < 0), temos a raiz de um número negativo aparecendo no denominador.
O correto seria se o exercício pedisse o limite quando x aproxima-se de 0 pela direita (ou seja, x > 0). Isto é, o exercício deveria ser:
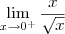
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Claudin » Qui Mai 19, 2011 12:31
por Claudin » Qui Mai 19, 2011 12:31
O exercicio foi esse msm Luiz.
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [limite] Dúvida limite com raizes
por rqaugusto » Dom Abr 30, 2017 23:23
- 0 Respostas
- 3111 Exibições
- Última mensagem por rqaugusto

Dom Abr 30, 2017 23:23
Cálculo: Limites, Derivadas e Integrais
-
- Limite - Duvida
por Claudin » Qua Mai 18, 2011 18:32
- 3 Respostas
- 2585 Exibições
- Última mensagem por Claudin

Qua Mai 18, 2011 20:45
Cálculo: Limites, Derivadas e Integrais
-
- Duvida - Limite
por Claudin » Qui Mai 19, 2011 09:20
- 5 Respostas
- 3063 Exibições
- Última mensagem por Claudin

Dom Mai 22, 2011 16:19
Cálculo: Limites, Derivadas e Integrais
-
- Duvida - Limite
por Claudin » Sáb Mai 21, 2011 16:17
- 18 Respostas
- 10887 Exibições
- Última mensagem por Claudin

Qui Mai 26, 2011 15:32
Cálculo: Limites, Derivadas e Integrais
-
- [LIMITE] duvida
por beel » Sáb Set 03, 2011 20:32
- 4 Respostas
- 1930 Exibições
- Última mensagem por beel

Dom Set 04, 2011 15:30
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 10 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\lim_{x\rightarrow0}\frac{x}{\sqrt[]{x}} \lim_{x\rightarrow0}\frac{x}{\sqrt[]{x}}](/latexrender/pictures/41d1c6f9cac6aa6e7731c6f6e1f48d03.png)
![\lim_{x\rightarrow0}\frac{x}{\sqrt[]{x}} . \frac{\sqrt[]{x}}{\sqrt[]{x}} \lim_{x\rightarrow0}\frac{x}{\sqrt[]{x}} . \frac{\sqrt[]{x}}{\sqrt[]{x}}](/latexrender/pictures/f39052e533faf1d814aff069e6616660.png)
![\lim_{x\rightarrow0}\frac{x.\sqrt[]{x}}{x} = \frac{\sqrt[]{x}}{0} = 0 \lim_{x\rightarrow0}\frac{x.\sqrt[]{x}}{x} = \frac{\sqrt[]{x}}{0} = 0](/latexrender/pictures/5e4c7fbb8e2ec20882e9e4b1738ceee0.png)
![\frac{0}{\sqrt[]{x}} \frac{0}{\sqrt[]{x}}](/latexrender/pictures/529f52e095fc9ce86bacfefa3040d087.png)
 ou
ou  ? E se fosse
? E se fosse ![\frac{1}{\sqrt[]{x}} \frac{1}{\sqrt[]{x}}](/latexrender/pictures/911233eacfdf6c16c12ac8d1e3dc6824.png) qual seria a resposta final?
qual seria a resposta final?
![\lim_{x\rightarrow0}\frac{x}{\sqrt[]{x}} \lim_{x\rightarrow0}\frac{x}{\sqrt[]{x}}](/latexrender/pictures/41d1c6f9cac6aa6e7731c6f6e1f48d03.png)
![\lim_{x\rightarrow0}\frac{x}{\sqrt[]{x}} . \frac{\sqrt[]{x}}{\sqrt[]{x}} \lim_{x\rightarrow0}\frac{x}{\sqrt[]{x}} . \frac{\sqrt[]{x}}{\sqrt[]{x}}](/latexrender/pictures/f39052e533faf1d814aff069e6616660.png)
![\lim_{x\rightarrow0}\frac{x.\sqrt[]{x}}{x} = \frac{\sqrt[]{x}}{0} = 0 \lim_{x\rightarrow0}\frac{x.\sqrt[]{x}}{x} = \frac{\sqrt[]{x}}{0} = 0](/latexrender/pictures/5e4c7fbb8e2ec20882e9e4b1738ceee0.png)
![\frac{0}{\sqrt[]{x}} \frac{0}{\sqrt[]{x}}](/latexrender/pictures/529f52e095fc9ce86bacfefa3040d087.png)
 ou
ou  ? E se fosse
? E se fosse ![\frac{1}{\sqrt[]{x}} \frac{1}{\sqrt[]{x}}](/latexrender/pictures/911233eacfdf6c16c12ac8d1e3dc6824.png) qual seria a resposta final?
qual seria a resposta final?
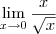 . Vamos trabalhar como potências:
. Vamos trabalhar como potências:
 a variável, é ela que tende a zero.
a variável, é ela que tende a zero.

![\frac{x.\sqrt[]{x}}{x} = \frac{\sqrt[]{x}}{1} \frac{x.\sqrt[]{x}}{x} = \frac{\sqrt[]{x}}{1}](/latexrender/pictures/d64719a654b11a507a6bd41534b143dd.png)