 por benni » Ter Mai 17, 2011 15:41
por benni » Ter Mai 17, 2011 15:41
Resolva o sistema de equações linear:

.

=

e discuta o significado geométrico do conjunto solução, se exixtir.
-
benni
- Usuário Dedicado

-
- Mensagens: 39
- Registrado em: Qua Mar 02, 2011 15:06
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matematica
- Andamento: formado
 por carlosalesouza » Ter Mai 17, 2011 17:50
por carlosalesouza » Ter Mai 17, 2011 17:50
Primeiramente, encontramos a Determinante.
Para isso, reproduzimos as 2 primeiras colunas à direita:
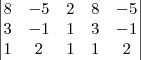
E somamos o produto das diagonais para a direita e subtraímos o das diagonais para a esquerda:
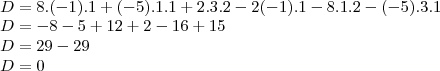
A Determinante é 0...
Substituindo a primeira coluna da matriz pela coluna depois da igualdade, neste caso, 0, 0 e 0, teremos a Dx, substituindo a segunda, teremos Dy e a terceira nos dará Dz...
Com isso, sabemos que
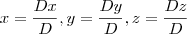
Entretanto, como sabemos que D = 0 e que 0 não é um divisor válido, logo, não existe conjunto solução...
Carlos Alexandre
Ciências Contábeis - FECEA/PR
Matemática - UEPG/PR
-
carlosalesouza
- Colaborador Voluntário

-
- Mensagens: 103
- Registrado em: Sex Abr 29, 2011 17:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática -LIC
- Andamento: cursando
 por MarceloFantini » Ter Mai 17, 2011 19:37
por MarceloFantini » Ter Mai 17, 2011 19:37
Pelo contrário, o conjunto solução é infinito. Veja que se fizermos

, já temos uma solução. Neste caso, o sistema é possível e indeterminado, pois existem inúmeras soluções.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por carlosalesouza » Qua Mai 18, 2011 00:11
por carlosalesouza » Qua Mai 18, 2011 00:11
Isso mesmo... rs foi gafe minha... estava saindo quando comecei a responder ao topico e acabei fazendo um serviço mal feito... rs
Depois pensei a respeito e vi meu erro... dai fiquei pensando... tenho que voltar pra casa pra responder certo aquele tópico... rs
O principal erro é que, apesar de D ser 0, que não pode ser divisor, Dx = Dy = Dz = 0, ou seja, teríamos 0/0, que cai em uma indeterminação...
Um abraço
Carlos Alexandre
Ciências Contábeis - FECEA/PR
Matemática - UEPG/PR
-
carlosalesouza
- Colaborador Voluntário

-
- Mensagens: 103
- Registrado em: Sex Abr 29, 2011 17:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática -LIC
- Andamento: cursando
 por benni » Qua Mai 18, 2011 13:00
por benni » Qua Mai 18, 2011 13:00
Obrigado pessoal pela ajuda, mas pensei assim
fiz a matriz aumentada adicionando a coluna do zero e por consequencia qualquer métodode resolução ira resultar em x = 0 , y = 0 e z = 0
como Det(A) = -12
Um sistema linear é homogêneo quando os termos independentes de todas as equações são nulos. Todo sistema linear homogêneo admite pelo menos a solução trivial, que é a solução identicamente nula. Assim, todo sistema linear homogêneo é possível. Este tipo de sistema poderá ser determinado se admitir somente a solução trivial ou indeterminado se admitir outras soluções além da trivial.
agora a analise geometrica,não consegui vizualizar?
-
benni
- Usuário Dedicado

-
- Mensagens: 39
- Registrado em: Qua Mar 02, 2011 15:06
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matematica
- Andamento: formado
 por carlosalesouza » Qui Mai 19, 2011 09:19
por carlosalesouza » Qui Mai 19, 2011 09:19
Admitindo um sistema determinado, com as variáveis igual a zero, a solução se posiciona no ponto (0,0,0) que é a origem do plano cartesiano tridimensinal...
- Anexos
-

- Solucao = Origem.png (2.88 KiB) Exibido 8802 vezes
Carlos Alexandre
Ciências Contábeis - FECEA/PR
Matemática - UEPG/PR
-
carlosalesouza
- Colaborador Voluntário

-
- Mensagens: 103
- Registrado em: Sex Abr 29, 2011 17:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática -LIC
- Andamento: cursando
 por MarceloFantini » Qui Mai 19, 2011 18:38
por MarceloFantini » Qui Mai 19, 2011 18:38
Esta é uma das soluções, mas não explica as outras. Para isto, é necessário saber que

é a equação de um plano, logo, se a única solução é a trivial, isso quer dizer três planos que se interceptam apenas na origem. Outras possibilidades são: três planos que tem uma reta em comum ou na verdade são o mesmo plano.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por arima » Qui Mai 19, 2011 21:29
por arima » Qui Mai 19, 2011 21:29
Eu fiz por esclonamento e fiz em função da variavel z.Deu duas equações e tres incognitas.Chamei z de alfa e as soluçoes ficaram em função de z.Portanto sistema possivel indeterminado com infinitas soluçoes.agora ta dififcil representar no plano pois não sei como trabalhar com winplot.
-
arima
- Usuário Parceiro

-
- Mensagens: 50
- Registrado em: Sáb Out 23, 2010 18:25
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matematica
- Andamento: cursando
 por arima » Qui Mai 19, 2011 21:34
por arima » Qui Mai 19, 2011 21:34
Eu fiz por esclonamento e fiz em função da variavel z.Deu duas equações e tres incognitas.Chamei z de alfa e as soluçoes ficaram em função de z.Portanto sistema possivel indeterminado com infinitas soluçoes.agora ta dififcil representar no plano pois não sei como trabalhar com winplot.
-
arima
- Usuário Parceiro

-
- Mensagens: 50
- Registrado em: Sáb Out 23, 2010 18:25
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matematica
- Andamento: cursando
 por lanca » Sáb Mai 21, 2011 18:26
por lanca » Sáb Mai 21, 2011 18:26
Pessoal vc chegaram em algo assim:
y= -2z/7 e x= -1z/14
-
lanca
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Dom Mai 15, 2011 00:15
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matematica
- Andamento: formado
 por lanca » Sáb Mai 21, 2011 22:59
por lanca » Sáb Mai 21, 2011 22:59
Oi benni!!!
Eu fiz por escalonamento e encontrei após refazer os cálculos que:
y= -2z/7 e x= -3z/7
-
lanca
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Dom Mai 15, 2011 00:15
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matematica
- Andamento: formado
 por arima » Dom Mai 22, 2011 17:33
por arima » Dom Mai 22, 2011 17:33
Eu também fiz assim.
-
arima
- Usuário Parceiro

-
- Mensagens: 50
- Registrado em: Sáb Out 23, 2010 18:25
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matematica
- Andamento: cursando
 por LuizAquino » Dom Mai 22, 2011 18:19
por LuizAquino » Dom Mai 22, 2011 18:19
A matriz ampliada do sistema é:
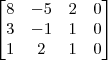
Façamos por escalonamento.
Primeiro, troque de posição a linha 1 com a linha 3.

Façamos:
linha 2 recebe: (linha 2) - 3*(linha 1)
linha 3 recebe: (linha 3) - 8*(linha 1)
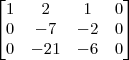
Façamos:
linha 3 recebe: (linha 3) - 3*(linha 2)
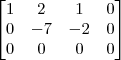
Façamos:
linha 1 recebe: 2*(linha 1) + (linha 2)

Logo, o sistema equivalente é:

Geometricamente, isso é a interseção de dois planos que resulta na reta:
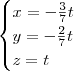
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Matrizes e Determinantes
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [sistema linear homogeneo] Como resolver esse sistema
por amigao » Qua Jul 02, 2014 14:49
- 1 Respostas
- 3079 Exibições
- Última mensagem por Russman

Qua Jul 02, 2014 18:38
Álgebra Linear
-
- [Sistema linear] Sistema linear com constante
por smlspirit » Qui Jul 19, 2012 19:34
- 4 Respostas
- 5543 Exibições
- Última mensagem por Russman

Qui Jul 19, 2012 22:40
Sistemas de Equações
-
- [Sistema Linear] MACK-SP: Sistema de Equações
por ALF » Sex Ago 26, 2011 13:24
- 1 Respostas
- 4486 Exibições
- Última mensagem por LuizAquino

Dom Ago 28, 2011 12:57
Sistemas de Equações
-
- Matrix X
 por rafaela5523 » Sex Mar 25, 2016 20:56
por rafaela5523 » Sex Mar 25, 2016 20:56
- 1 Respostas
- 5507 Exibições
- Última mensagem por rafaela5523

Sex Mar 25, 2016 21:17
Matrizes e Determinantes
-
- [Matrix do operador]
por Tathiclau » Sáb Dez 14, 2013 14:37
- 4 Respostas
- 4057 Exibições
- Última mensagem por Tathiclau

Sáb Dez 14, 2013 19:09
Álgebra Linear
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 .
.  =
= 

 .
.  =
= 

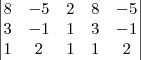
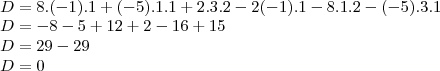
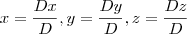

 , já temos uma solução. Neste caso, o sistema é possível e indeterminado, pois existem inúmeras soluções.
, já temos uma solução. Neste caso, o sistema é possível e indeterminado, pois existem inúmeras soluções.




 é a equação de um plano, logo, se a única solução é a trivial, isso quer dizer três planos que se interceptam apenas na origem. Outras possibilidades são: três planos que tem uma reta em comum ou na verdade são o mesmo plano.
é a equação de um plano, logo, se a única solução é a trivial, isso quer dizer três planos que se interceptam apenas na origem. Outras possibilidades são: três planos que tem uma reta em comum ou na verdade são o mesmo plano.






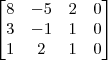

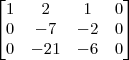
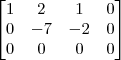


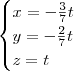



 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.