o resultado nao foi exato!
Por exemplo
![\lim_{x\rightarrow+\infty}\sqrt[]{x^2+7x}-x \lim_{x\rightarrow+\infty}\sqrt[]{x^2+7x}-x](/latexrender/pictures/85afe7dfeb95a1acff77906b9e41b8ff.png)
a forma estratégica pela qual vc adotou no video foi de multiplicar e dividir a expressao por
![\sqrt[]{x^2+7x}-x \sqrt[]{x^2+7x}-x](/latexrender/pictures/b306f68273406fce9890ef2d6097bbe9.png)
e dps da multiplicação e divisão, dividir tanto o numerador quanto o denominador por x, oq resultou em

Porém eu tentei fazer dividindo logo de cara, por x, e não consegui chegar no mesmo resultado
entao eu gostaria de saber, essas estrategias para resolução sao pela lógica e pela suposição nao é? Ou tem alguma
forma de análise que facilite, encontrar a estrategia exata, se é que existe uma estratégia exata. (podem ter outras, claro!)
obrigado


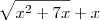 .
.

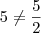 .
.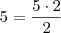 .
.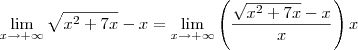

 . Isso significa que nesse caso essa estratégia não é útil para nos levar na solução do exercício.
. Isso significa que nesse caso essa estratégia não é útil para nos levar na solução do exercício.
 ?
?![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)