 por Giles » Qua Out 29, 2008 23:24
por Giles » Qua Out 29, 2008 23:24
Seja
![M = {[{a}_{ij}]}_{nxn} M = {[{a}_{ij}]}_{nxn}](/latexrender/pictures/10509744a774c268fa3ff8e8299b6d2b.png)
uma matriz quadrada de ordem n, onde aij= i + j. Nessas condições, a soma dos elementos da diagonal principal dessa matriz é:
a -) n²
b-) 2n + 2n²
c-) 2n + n²
d-) n² + n
e-) n + 2n²
OBS.:
Soma dos n primeiros termos de uma PA:

Soma dos n primeiros termos de uma PG:

Outra que não consegui resolver:
Considere a matriz A = [2 -1] e uma matriz
![B = [{b}_{ij}] B = [{b}_{ij}]](/latexrender/pictures/c8e53792e5e45c41b0a1935b458435d1.png)
. Se A . B. A = A, então é correto afirmar que a matriz B:
a-)

b-)
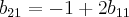
c-)
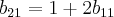
d-)
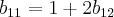
e-)

Agradeço a atenção!
"As pessoas que vencem nessa vida são aquelas que procuram as circunstâncias de que precisam e quando não as encontram, as criam"
-

Giles
- Usuário Ativo

-
- Mensagens: 17
- Registrado em: Dom Out 19, 2008 11:14
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Curso Técnico em Construção Civil Integr
- Andamento: cursando
 por Molina » Qua Out 29, 2008 23:45
por Molina » Qua Out 29, 2008 23:45
Giles escreveu:Seja
![M = {[{a}_{ij}]}_{nxn} M = {[{a}_{ij}]}_{nxn}](/latexrender/pictures/10509744a774c268fa3ff8e8299b6d2b.png)
uma matriz quadrada de ordem n, onde aij= i + j. Nessas condições, a soma dos elementos da diagonal principal dessa matriz é:
a -) n²
b-) 2n + 2n²
c-) 2n + n²
d-) n² + n
e-) n + 2n²
OBS.:
Soma dos n primeiros termos de uma PA:

Soma dos n primeiros termos de uma PG:

A diagonal principal é formada por membros onde i = j.
Ou seja, 1+1, 2+2, 3+3, 4+4, ... , n+n => 2, 4, 6, 8, ... , 2n
Logo a sequencia a cima é uma PA de razão 2.
Usando a fórmula da Soma da PA:

Resposta: letra d
Se nao houve erro nas contas, é isso.
Abraços.
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Giles » Qui Out 30, 2008 00:11
por Giles » Qui Out 30, 2008 00:11
molina escreveu:Giles escreveu:Seja
![M = {[{a}_{ij}]}_{nxn} M = {[{a}_{ij}]}_{nxn}](/latexrender/pictures/10509744a774c268fa3ff8e8299b6d2b.png)
uma matriz quadrada de ordem n, onde aij= i + j. Nessas condições, a soma dos elementos da diagonal principal dessa matriz é:
a -) n²
b-) 2n + 2n²
c-) 2n + n²
d-) n² + n
e-) n + 2n²
OBS.:
Soma dos n primeiros termos de uma PA:

Soma dos n primeiros termos de uma PG:

A diagonal principal é formada por membros onde i = j.
Ou seja, 1+1, 2+2, 3+3, 4+4, ... , n+n => 2, 4, 6, 8, ... , 2n
Logo a sequencia a cima é uma PA de razão 2.
Usando a fórmula da Soma da PA:

Resposta: letra d
Se nao houve erro nas contas, é isso.
Abraços.
Obrigado Molina... Sua resposta está corretíssima! Muito obrigado!
Grande abraço!
Giles. "As pessoas que vencem nessa vida são aquelas que procuram as circunstâncias de que precisam e quando não as encontram, as criam"
-

Giles
- Usuário Ativo

-
- Mensagens: 17
- Registrado em: Dom Out 19, 2008 11:14
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Curso Técnico em Construção Civil Integr
- Andamento: cursando
 por Molina » Qui Out 30, 2008 00:20
por Molina » Qui Out 30, 2008 00:20
Giles, de nada!
Confirme apenas se na segunda atividade é A
(vezes) B
(vezes) A
(igual) A
Abraços e bom estudo

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Giles » Qui Out 30, 2008 00:29
por Giles » Qui Out 30, 2008 00:29
É isso mesmo! (Y)
"As pessoas que vencem nessa vida são aquelas que procuram as circunstâncias de que precisam e quando não as encontram, as criam"
-

Giles
- Usuário Ativo

-
- Mensagens: 17
- Registrado em: Dom Out 19, 2008 11:14
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Curso Técnico em Construção Civil Integr
- Andamento: cursando
 por diegodalcol » Qui Nov 13, 2008 23:53
por diegodalcol » Qui Nov 13, 2008 23:53
estou com a seginte duvida na soma dessas duas matrizes:

meu resultado foi:

será que fiz certo?
-
diegodalcol
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qui Mai 22, 2008 13:06
- Área/Curso: Estudante
- Andamento: cursando
 por Molina » Sex Nov 14, 2008 01:21
por Molina » Sex Nov 14, 2008 01:21
diegodalcol escreveu:estou com a seginte duvida na soma dessas duas matrizes:

meu resultado foi:

será que fiz certo?
Olá Diego.
A primeira matriz é

e a segunda é

, certo?
c(i,j) = a(i,j) + b(i,j)
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Molina » Sex Nov 14, 2008 01:24
por Molina » Sex Nov 14, 2008 01:24
diegodalcol escreveu:estou com a seginte duvida na soma dessas duas matrizes:

meu resultado foi:

será que fiz certo?
Olá Diego.
A primeira matriz é

e a segunda é
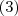
, certo?
A soma de matrizes só está definida para matrizes de mesma ordem,
e as matrizes a cima nao possuem mesma ordem.
Então nao tem sentido somar uma matriz 1x3 com outra 1x1.
Bom estudo!

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Matrizes e Determinantes
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Matrizes invertíveis] e matrizes inversas
por JacquesPhilippe » Seg Ago 08, 2011 19:19
- 3 Respostas
- 5152 Exibições
- Última mensagem por LuizAquino

Qui Ago 11, 2011 19:43
Matrizes e Determinantes
-
- [Matrizes] produto de matrizes
 por vanessafey » Dom Ago 28, 2011 16:54
por vanessafey » Dom Ago 28, 2011 16:54
- 1 Respostas
- 3594 Exibições
- Última mensagem por MarceloFantini

Dom Ago 28, 2011 17:35
Matrizes e Determinantes
-
- [MATRIZES] Demonstração de matrizes
por farinha99 » Sáb Set 03, 2016 11:56
- 0 Respostas
- 5997 Exibições
- Última mensagem por farinha99

Sáb Set 03, 2016 11:56
Matrizes e Determinantes
-
- matrizes
por luix henrique » Seg Out 13, 2008 15:42
- 1 Respostas
- 9686 Exibições
- Última mensagem por Molina

Seg Out 13, 2008 20:13
Matrizes e Determinantes
-
- Matrizes
por Cleyson007 » Sáb Nov 01, 2008 00:51
- 2 Respostas
- 3041 Exibições
- Última mensagem por Cleyson007

Sex Mai 29, 2009 11:14
Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![M = {[{a}_{ij}]}_{nxn} M = {[{a}_{ij}]}_{nxn}](/latexrender/pictures/10509744a774c268fa3ff8e8299b6d2b.png) uma matriz quadrada de ordem n, onde aij= i + j. Nessas condições, a soma dos elementos da diagonal principal dessa matriz é:
uma matriz quadrada de ordem n, onde aij= i + j. Nessas condições, a soma dos elementos da diagonal principal dessa matriz é:

![B = [{b}_{ij}] B = [{b}_{ij}]](/latexrender/pictures/c8e53792e5e45c41b0a1935b458435d1.png) . Se A . B. A = A, então é correto afirmar que a matriz B:
. Se A . B. A = A, então é correto afirmar que a matriz B:
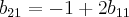
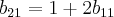
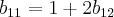









 e a segunda é
e a segunda é  , certo?
, certo?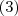 , certo?
, certo?