jamiel, não sei se é o que vc está precisando saber... mas...
Uma função ou equação esponencial é dada por
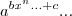
e por aí a fora.... rs pode se estender ao infinito... rs
Como podemos notar só de bater o olho, não é lá muito cômodo desenvolvê-la ou simplificá-la assim como está...
Então, seguindo o princípio da igualdade, podemos substituir uma variável (ou até um valor mais complicado, como um logaritmo) por outra variável qualquer, que podemos arbitrar... assim, dizemos que
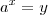
... eu, particularmente, prefiro por z... mas vc pode escolher qualquer letra ou símbolo, desde que vc declare na resolução (isso tbm não é obrigatório, só fica mais fácil de entender seu raciocínio)...
Assim, depois de substituir, vc terá situações do tipo... tudo bem que

, mas quando será
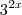
?
Daí vc faz:
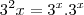
e sendo

, então

... do mesmo modo...
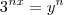
...
Depois de substituir, vc terá uma função ou equação regular, não uma exponencial... então vc pode fazer todas as operações devidas e chegar até onde vc possa... se for pra simplificar, vai até não ter mais pra onde ir... se for uma equação, vai até encontrar os valores de y, z, w ou seja lá qual for a variável que vc escolheu... então, vc pega os valores válidos encontrados e substitui novamente a variável por
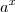
e vc poderá encontrar o valor de x...
Note que não há necessidade de y>0... mas,

sim e sendo y<0, então
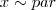
...
x não pode ser par porque
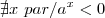
, certo?
Se te compliquei mais, dá um grito... kkkk









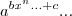 e por aí a fora.... rs pode se estender ao infinito... rs
e por aí a fora.... rs pode se estender ao infinito... rs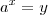 ... eu, particularmente, prefiro por z... mas vc pode escolher qualquer letra ou símbolo, desde que vc declare na resolução (isso tbm não é obrigatório, só fica mais fácil de entender seu raciocínio)...
... eu, particularmente, prefiro por z... mas vc pode escolher qualquer letra ou símbolo, desde que vc declare na resolução (isso tbm não é obrigatório, só fica mais fácil de entender seu raciocínio)... , mas quando será
, mas quando será 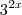 ?
?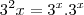 e sendo
e sendo  , então
, então  ... do mesmo modo...
... do mesmo modo... 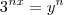 ...
...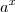 e vc poderá encontrar o valor de x...
e vc poderá encontrar o valor de x... sim e sendo y<0, então
sim e sendo y<0, então 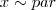 ...
...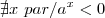 , certo?
, certo?




 .
.



