
Gostaria, se possível, de alguém para comentar essa resolução, e mais, me ajudar um pouco sobre o porquê de transformar em y, não assimilei bem isso, até agora. Agradeço qualquer ajuda!








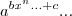 e por aí a fora.... rs pode se estender ao infinito... rs
e por aí a fora.... rs pode se estender ao infinito... rs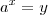 ... eu, particularmente, prefiro por z... mas vc pode escolher qualquer letra ou símbolo, desde que vc declare na resolução (isso tbm não é obrigatório, só fica mais fácil de entender seu raciocínio)...
... eu, particularmente, prefiro por z... mas vc pode escolher qualquer letra ou símbolo, desde que vc declare na resolução (isso tbm não é obrigatório, só fica mais fácil de entender seu raciocínio)... , mas quando será
, mas quando será 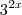 ?
?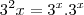 e sendo
e sendo  , então
, então  ... do mesmo modo...
... do mesmo modo... 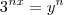 ...
...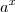 e vc poderá encontrar o valor de x...
e vc poderá encontrar o valor de x... sim e sendo y<0, então
sim e sendo y<0, então 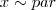 ...
...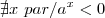 , certo?
, certo?



Voltar para Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
zig escreveu:

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.