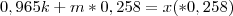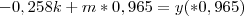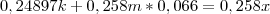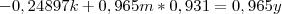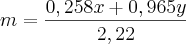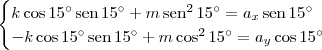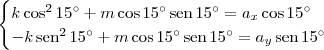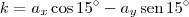por filduarte » Seg Mai 02, 2011 12:57
por filduarte » Seg Mai 02, 2011 12:57
Olá, preciso de ajuda. Já quebrei a cabeça mas não consigo resolver este problema. Eu tenho um retângulo com outros retângulos dentro. O retângulo principal gira 15º e eu preciso descobrir a distância do vértice mais distante dos retângulo internos em relação ao retângulo original (antes de ser rotacionado). Segue imagem para facilitar a compreensão:

As variáveis que são conhecidas são:
- x (largura do retângulo principal);
- y (altura do retângulo principal);
- ax (distância no eixo x do vértices do retângulo interno antes da rotação);
- ay (distância no eixo y do vértices do retângulo interno antes da rotação);
- w (largura do retângulo interno);
- h (altura do retângulo interno);
Preciso descobrir bx e by. Já tentei utilizando razões trigonométricas, mas não dá certo.
-
filduarte
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Seg Mai 02, 2011 12:37
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Desenho Industrial
- Andamento: cursando
 por FilipeCaceres » Seg Mai 02, 2011 20:44
por FilipeCaceres » Seg Mai 02, 2011 20:44
Rotacionar os eixos de um ângulo

e escrever as novas coordenadas de C são equivalentes a escrever as coordenadas de C' (vetor rotacionado em
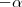
) no sistema original. Observe a figura

- rotacao.png (5.11 KiB) Exibido 2887 vezes
Assim temos,


Assim temos,

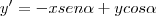
Espero que tenha entendido, com isso acho que seja suficiente para você resolver a sua questão.
Qualquer dúvida poste novamente.
Abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por LuizAquino » Seg Mai 02, 2011 22:12
por LuizAquino » Seg Mai 02, 2011 22:12
Aplicando a sugestão de
FilipeCaceres, podemos rearrumar o problema original como ilustra a figura abaixo.
Note que no sistema xOy as coordenadas de A são (ax, ay). Além disso, note que no sistema x'Oy' as coordenadas de B também são (ax, ay).
O que você deseja é descobrir as coordenadas de B em relação ao sistema xOy. Suponha que essas coordenadas sejam (k, m).
Substituindo essas informações no sistema de equações indicado, teremos:
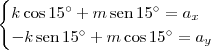
Agora, basta você resolver esse sistema para encontrar
k e
m.
Por fim, note que usando a notação da figura original, temos que

e
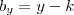
.
Em seu perfil consta que você é aluno do curso de Desenho Industrial. Esse problema que você quer resolver surgiu em algum projeto que você está trabalhando?
ObservaçãoNa disciplina de Geometria Analítica estudamos a rotação de eixos e a mudança de coordenadas. Eu recomendo que você procure por materiais ou livros dessa disciplina.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por filduarte » Ter Mai 03, 2011 13:56
por filduarte » Ter Mai 03, 2011 13:56
LuizAquino escreveu:Em seu perfil consta que você é aluno do curso de Desenho Industrial. Esse problema que você quer resolver surgiu em algum projeto que você está trabalhando?
Sim o problema surgiu durante um projeto. O tal retângulo externo que falei é um movieclip do flash e os retângulos menores são fotos. O que eu preciso é descobrir os pontos das fotos que ficam mais perto das extremidades esquerda, direita, superior e inferior. O exemplo que dei foi do ponto mais à direita.
Confesso que não consegui resolver o sistema (tentei pelo método da comparação) e peço a paciência de vocês para me ajudar a resolvê-lo. Para facilitar as coisas vamos assumir que
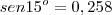
e

:
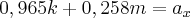
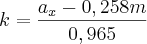
Substituindo na segunda equação:

Pois é, mas eu empaco aí. Não me lembro como inverter a equação quando tenho uma divisão de uma equação. Ficaria assim?

-
filduarte
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Seg Mai 02, 2011 12:37
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Desenho Industrial
- Andamento: cursando
 por LuizAquino » Ter Mai 03, 2011 15:50
por LuizAquino » Ter Mai 03, 2011 15:50
É mais fácil você resolver o sistema pelo método da soma.
Basta você multiplicar a primeira equação por
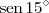
e a segunda por
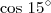
. Somando as duas equações resultantes, você irá determinar m.
Em seguida, basta você multiplicar a primeira equação por
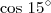
e a segunda por
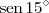
. Somando as duas equações resultantes, você irá determinar k.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por filduarte » Sex Mai 06, 2011 11:56
por filduarte » Sex Mai 06, 2011 11:56
Valeu pela ajuda! Consegui resolver. Só não entendi uma coisa:
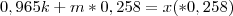
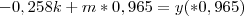
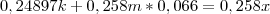
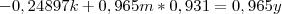
Aí a soma daria:

Ou seja:
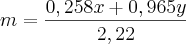
Só que essa expressão estava dando errado, até que percebi que se eu não dividisse por 2,22 ela dava certo. Onde está o meu erro?
Mais uma coisa: não entendi por que você disse que para descobrir k eu precisava multiplicar a primeira equação por cos15º e a segunda por sen15º. Bastou eu substituir o m numa das equações do sistema original e resolvi o problema.
-
filduarte
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Seg Mai 02, 2011 12:37
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Desenho Industrial
- Andamento: cursando
 por LuizAquino » Sex Mai 06, 2011 12:26
por LuizAquino » Sex Mai 06, 2011 12:26
Você errou aqui:
0,24897k + 0,258m * 0,066 = 0,258x
-0,24897k + 0,965m * 0,931 = 0,965y
Deveria ficar apenas com:
0,24897k + 0,066m = 0,258x
-0,24897k + 0,931m = 0,965y
Agora, vejamos a resolução usando a minha sugestão.
Primeira parte
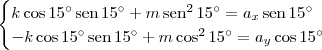

 Segunda parte
Segunda parte
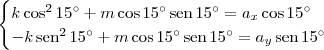

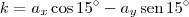 Observação
ObservaçãoÉ óbvio que poderíamos ter usado a expressão determinada para m na primeira etapa para determinar o k na segunda etapa. Mas, eu prefiro fazer esse exercício assim, pois as expressões para k e m ficam mais simples.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por filduarte » Sex Mai 06, 2011 12:51
por filduarte » Sex Mai 06, 2011 12:51
Entendi. Realmente dei mole na hora da multiplicação.
Mais uma vez agradeço pela paciência e pela ajuda!
Abraços!
-
filduarte
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Seg Mai 02, 2011 12:37
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Desenho Industrial
- Andamento: cursando
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- rotação de eixos
por CarolMarques » Sáb Set 01, 2012 19:38
- 4 Respostas
- 3537 Exibições
- Última mensagem por e8group

Dom Set 02, 2012 13:27
Geometria Analítica
-
- volume de sólido por rotação
por hmspriss » Qui Set 23, 2010 11:13
- 1 Respostas
- 2610 Exibições
- Última mensagem por MarceloFantini

Sex Set 24, 2010 01:32
Cálculo: Limites, Derivadas e Integrais
-
- [CONICAS] rotação e translação
por amigao » Sex Jun 28, 2013 19:31
- 1 Respostas
- 1183 Exibições
- Última mensagem por e8group

Sex Jul 12, 2013 12:00
Geometria Analítica
-
- Integrais - Volume por Rotação
por elisafrombrazil » Dom Abr 16, 2017 11:17
- 0 Respostas
- 4819 Exibições
- Última mensagem por elisafrombrazil

Dom Abr 16, 2017 11:17
Cálculo: Limites, Derivadas e Integrais
-
- Rotação-Superficie de Revolução
por DGM » Ter Dez 05, 2017 00:37
- 0 Respostas
- 1790 Exibições
- Última mensagem por DGM

Ter Dez 05, 2017 00:37
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 e escrever as novas coordenadas de C são equivalentes a escrever as coordenadas de C' (vetor rotacionado em
e escrever as novas coordenadas de C são equivalentes a escrever as coordenadas de C' (vetor rotacionado em 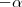 ) no sistema original. Observe a figura
) no sistema original. Observe a figura


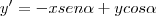

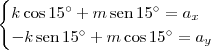
 e
e 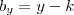 .
.
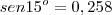 e
e  :
: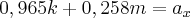
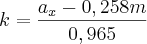


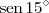 e a segunda por
e a segunda por 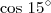 . Somando as duas equações resultantes, você irá determinar m.
. Somando as duas equações resultantes, você irá determinar m.