Aplicando a sugestão de
FilipeCaceres, podemos rearrumar o problema original como ilustra a figura abaixo.
Note que no sistema xOy as coordenadas de A são (ax, ay). Além disso, note que no sistema x'Oy' as coordenadas de B também são (ax, ay).
O que você deseja é descobrir as coordenadas de B em relação ao sistema xOy. Suponha que essas coordenadas sejam (k, m).
Substituindo essas informações no sistema de equações indicado, teremos:
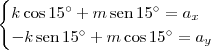
Agora, basta você resolver esse sistema para encontrar
k e
m.
Por fim, note que usando a notação da figura original, temos que

e
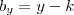
.
Em seu perfil consta que você é aluno do curso de Desenho Industrial. Esse problema que você quer resolver surgiu em algum projeto que você está trabalhando?
ObservaçãoNa disciplina de Geometria Analítica estudamos a rotação de eixos e a mudança de coordenadas. Eu recomendo que você procure por materiais ou livros dessa disciplina.



 e escrever as novas coordenadas de C são equivalentes a escrever as coordenadas de C' (vetor rotacionado em
e escrever as novas coordenadas de C são equivalentes a escrever as coordenadas de C' (vetor rotacionado em 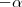 ) no sistema original. Observe a figura
) no sistema original. Observe a figura


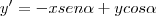

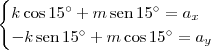
 e
e 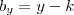 .
.
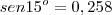 e
e  :
: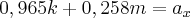
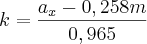


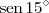 e a segunda por
e a segunda por 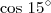 . Somando as duas equações resultantes, você irá determinar m.
. Somando as duas equações resultantes, você irá determinar m.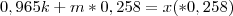
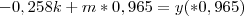
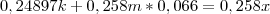
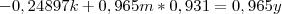

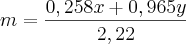

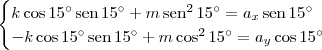



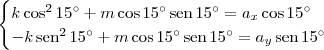

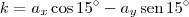
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
