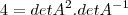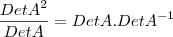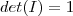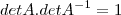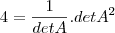por DanielRJ » Ter Mai 03, 2011 21:23
por DanielRJ » Ter Mai 03, 2011 21:23
127- Se A é uma matriz quadrada de ordem 2, inversivel, e det(A) o seu determinante. Se
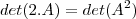
então det(A) será igual a:
a)0
b)1
c)1\2
d)4
Por hoje é só.
-

DanielRJ
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Sex Ago 20, 2010 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por FilipeCaceres » Ter Mai 03, 2011 22:05
por FilipeCaceres » Ter Mai 03, 2011 22:05
Sabendo que:

, para matriz A de ordem n.
Questão:
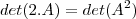
Para uma matriz


Logo,

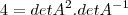
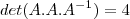
Como,

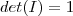
Temos,
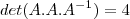

Portanto,

Espero que seja isso.
Editado pela última vez por
FilipeCaceres em Qui Mai 05, 2011 21:48, em um total de 2 vezes.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por DanielRJ » Qua Mai 04, 2011 10:23
por DanielRJ » Qua Mai 04, 2011 10:23
Pow mesma propriedade denovo valeu ae.
-

DanielRJ
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Sex Ago 20, 2010 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por DanielRJ » Qui Mai 05, 2011 20:05
por DanielRJ » Qui Mai 05, 2011 20:05
Filipe só me explica uma coisa de onde surguiu o
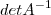
?? desde já obrigado!
-

DanielRJ
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Sex Ago 20, 2010 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por FilipeCaceres » Qui Mai 05, 2011 20:47
por FilipeCaceres » Qui Mai 05, 2011 20:47
Você quer saber nesta passagem
Observe o que eu fiz,


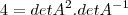
Abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por FilipeCaceres » Qui Mai 05, 2011 21:41
por FilipeCaceres » Qui Mai 05, 2011 21:41
Sabendo que

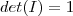
Temos,

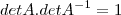

Como temos,

Então,
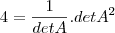
Portanto,

Abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
Voltar para Matrizes e Determinantes
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Nível fácil - FCC e UPE
por ingridgusmao » Dom Jun 12, 2011 02:41
- 1 Respostas
- 7533 Exibições
- Última mensagem por nietzsche

Sex Jun 24, 2011 22:54
Conjuntos
-
- Conjuntos - ITA nível fácil
por ingridgusmao » Qua Mai 25, 2011 01:46
- 2 Respostas
- 3116 Exibições
- Última mensagem por ingridgusmao

Qua Mai 25, 2011 02:21
Conjuntos
-
- UNIVASF - nível fácil
por ingridgusmao » Qua Jun 08, 2011 13:56
- 1 Respostas
- 1376 Exibições
- Última mensagem por Neperiano

Ter Ago 23, 2011 17:39
Funções
-
- Determinantes Nivel medio
por DanielRJ » Ter Mai 03, 2011 21:17
- 1 Respostas
- 1567 Exibições
- Última mensagem por FilipeCaceres

Ter Mai 03, 2011 21:59
Matrizes e Determinantes
-
- OBM - Nível 1
 por Molina » Qui Jun 11, 2009 21:38
por Molina » Qui Jun 11, 2009 21:38
- 3 Respostas
- 2875 Exibições
- Última mensagem por Molina

Dom Jun 14, 2009 14:38
Desafios Fáceis
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
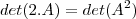 então det(A) será igual a:
então det(A) será igual a:
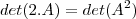 então det(A) será igual a:
então det(A) será igual a:
 , para matriz A de ordem n.
, para matriz A de ordem n.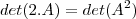



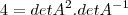
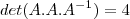

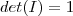
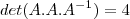




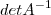 ?? desde já obrigado!
?? desde já obrigado!