 por suziquim » Qui Mai 05, 2011 15:53
por suziquim » Qui Mai 05, 2011 15:53
-
suziquim
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Qui Mai 05, 2011 11:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia
- Andamento: cursando
 por Abelardo » Qui Mai 05, 2011 16:45
por Abelardo » Qui Mai 05, 2011 16:45
Eu não sei qual é o conjunto universo que a questão trabalha, mas me ''
parece'' que, dada a igualdade inicial

, os únicos valores que x pode assumir é zero e um.
Pelo que sei, trabalhando no conjunto do reais, para uma potência ter resultado igual a 1, ela deve ser elevada a zero ou sua base ser 1.

![1^3=1^{0,5} \to 1^3=1^{\frac{5}{10}} \to 1^3 = \sqrt[10]{1^5} \to 1=1 1^3=1^{0,5} \to 1^3=1^{\frac{5}{10}} \to 1^3 = \sqrt[10]{1^5} \to 1=1](/latexrender/pictures/37c0b842983add215b84d4a55cfc48c7.png) Espero que algum amigo do fórum apareça para ver se o que eu disse é válido
Espero que algum amigo do fórum apareça para ver se o que eu disse é válido.
-

Abelardo
- Colaborador Voluntário

-
- Mensagens: 159
- Registrado em: Qui Mar 03, 2011 01:45
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por suziquim » Qui Mai 05, 2011 17:21
por suziquim » Qui Mai 05, 2011 17:21
Entendi...a minha dúvida estava justamente no x elevado a 2,5, mas realmente o que você escreveu tem sentido.
Obrigada
-
suziquim
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Qui Mai 05, 2011 11:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Sistema entre Máximo Divisor Comum e Mínimo Múltiplo Comum
por Guga1981 » Qua Jan 21, 2015 22:21
- 2 Respostas
- 2301 Exibições
- Última mensagem por Guga1981

Qui Jan 22, 2015 21:28
Equações
-
- Ponto em que duas funções se interceptam
por Fernanda Lauton » Dom Jun 13, 2010 18:14
- 7 Respostas
- 7865 Exibições
- Última mensagem por Fernanda Lauton

Seg Jun 14, 2010 16:15
Funções
-
- [Minimização de funções] Distância entre duas retas reversas
por guisaulo » Sáb Jun 08, 2013 14:48
- 2 Respostas
- 2593 Exibições
- Última mensagem por guisaulo

Sáb Jun 08, 2013 16:48
Cálculo: Limites, Derivadas e Integrais
-
- Máximo divisor comum e mínimo múltiplo comum
por danizinha2000 » Qua Out 17, 2012 18:15
- 1 Respostas
- 1756 Exibições
- Última mensagem por Cleyson007

Qua Out 17, 2012 19:25
Álgebra Elementar
-
- Relação entre duas fórmulas
por FelipeScheidemantel » Qui Mar 19, 2009 19:19
- 0 Respostas
- 1758 Exibições
- Última mensagem por FelipeScheidemantel

Qui Mar 19, 2009 19:19
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


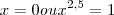



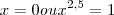

 , os únicos valores que x pode assumir é zero e um.
, os únicos valores que x pode assumir é zero e um.
![1^3=1^{0,5} \to 1^3=1^{\frac{5}{10}} \to 1^3 = \sqrt[10]{1^5} \to 1=1 1^3=1^{0,5} \to 1^3=1^{\frac{5}{10}} \to 1^3 = \sqrt[10]{1^5} \to 1=1](/latexrender/pictures/37c0b842983add215b84d4a55cfc48c7.png)




 , avisa que eu resolvo.
, avisa que eu resolvo.

