 por Diana » Ter Mai 03, 2011 00:11
por Diana » Ter Mai 03, 2011 00:11
Um comerciante deu um desconto de 20% sobre o preço de venda de uma mercadoria e, mesmo assim, conseguiu um lucro de 20% sobre o preço que pagou pela mesma. se o desconto nao fosse dado, qual seria seu lucro, em porcentagem?
- Eu tentei de tudo, eu nao sei o que eu calculo com o que, só a explicação já seria de mais!
-
Diana
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Ter Mai 03, 2011 00:03
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Abelardo » Ter Mai 03, 2011 13:26
por Abelardo » Ter Mai 03, 2011 13:26
Chamemos de x o preço de venda da mercadoria.
Chamemos de y o preço que o comerciante pagou para comprar o produto.
1º 20% de desconto em x é o mesmo que vender a mercadoria por

--> O comprador pagará por 80% do verdadeiro valor da mercadoria

-->

2º Mesmo vendendo com 20% de desconto a mercadoria, ele conseguiu um lucro de 20% sobre o preço de compra do produto ( y ). -->

, logo

.
3º Isolando x encontramos a seguinte relação -->
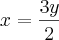
. Podemos transformando

em
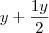
. Logo, vendendo a mercadoria por x ( Sem desconto) o comerciante ganhará o mesmo que y + 1y/2, o que significa que ele lucrará 1y/2 que é o mesmo que 50%.
Você tem o gabarito?
-

Abelardo
- Colaborador Voluntário

-
- Mensagens: 159
- Registrado em: Qui Mar 03, 2011 01:45
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Diana » Ter Mai 03, 2011 20:06
por Diana » Ter Mai 03, 2011 20:06
Meio confuso, mas eu entendi eu acho. obrigada

tenho as respostas,mas não o gabarito comentado, e deu certinho, obrigada mesmo!
-
Diana
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Ter Mai 03, 2011 00:03
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por FilipeCaceres » Ter Mai 03, 2011 20:33
por FilipeCaceres » Ter Mai 03, 2011 20:33
Olá Diana,
Sempre que postar uma questão não se esqueça de postar o gabarito junto,caso o tenha. Desta forma, você evitará um possível erro de quem estiver postando a solução.
Abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
Voltar para Matemática Financeira
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- problema da UFF de porcentagem
por vanessacosta » Sáb Jun 27, 2009 16:56
- 1 Respostas
- 14317 Exibições
- Última mensagem por Roberta

Seg Jun 29, 2009 21:04
Matemática Financeira
-
- [Problema com porcentagem]
por Pstefani » Ter Set 06, 2011 14:46
- 5 Respostas
- 4800 Exibições
- Última mensagem por Pstefani

Sex Set 09, 2011 22:37
Desafios Fáceis
-
- Problema de porcentagem!
por LuizCarlos » Sáb Set 10, 2011 17:57
- 1 Respostas
- 1797 Exibições
- Última mensagem por Neperiano

Sáb Set 10, 2011 22:02
Álgebra Elementar
-
- Problema com porcentagem
por danielrgoes » Ter Mai 29, 2012 20:50
- 1 Respostas
- 1814 Exibições
- Última mensagem por Neperiano

Ter Jun 05, 2012 18:44
Funções
-
- problema de porcentagem
por fna » Seg Mai 27, 2013 04:39
- 0 Respostas
- 2037 Exibições
- Última mensagem por fna

Seg Mai 27, 2013 04:39
Aritmética
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 --> O comprador pagará por 80% do verdadeiro valor da mercadoria
--> O comprador pagará por 80% do verdadeiro valor da mercadoria  -->
--> 
 , logo
, logo  .
. 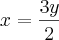 . Podemos transformando
. Podemos transformando  em
em 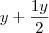 . Logo, vendendo a mercadoria por x ( Sem desconto) o comerciante ganhará o mesmo que y + 1y/2, o que significa que ele lucrará 1y/2 que é o mesmo que 50%.
. Logo, vendendo a mercadoria por x ( Sem desconto) o comerciante ganhará o mesmo que y + 1y/2, o que significa que ele lucrará 1y/2 que é o mesmo que 50%.

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.