 na figura abaixo.
na figura abaixo.


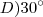

Gabarito: C
Alguém tem alguma dica.

 na figura abaixo.
na figura abaixo.


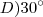




 , pois
, pois  e
e  são minhas bissetrizes externas, logo o ângulo
são minhas bissetrizes externas, logo o ângulo 

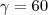
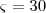



 seria construir uma cincunferência de raio
seria construir uma cincunferência de raio  desta forma observaríamos que o ponto F perntence a cincunferência, portanto,
desta forma observaríamos que o ponto F perntence a cincunferência, portanto, 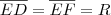 .
.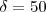


Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante

 .
.
 :
: