 por FilipeCaceres » Sex Abr 29, 2011 23:17
por FilipeCaceres » Sex Abr 29, 2011 23:17
Ressuscitando um morto,rsrs
Fora de escala.
Vejam o que eu fiz, mas ainda não consegui provar certas coisas, espero que colocando este meu rascunho possa despertar alguma ideia em alguém.
Dados da minha figura.



, pois

e

são minhas bissetrizes externas, logo o ângulo

Minhas bissetrizes externas valem

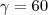
Portanto,
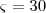

É possível encontrar outros ângulos, mas optei postar apenas estes pois os demais são fáceis de se ver.
Alguém teria alguma dica para provar que

Agradeço desde já.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por FilipeCaceres » Sáb Abr 30, 2011 22:47
por FilipeCaceres » Sáb Abr 30, 2011 22:47
Uma forma de mostrar que

seria construir uma cincunferência de raio

desta forma observaríamos que o ponto F perntence a cincunferência, portanto,
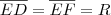
.
Tendo feito isso, temos
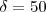
Portanto,

Espero que alguém tenha uma forma mais elegante de resolver esta questão.
Abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [trigonometria] trigonometria em triangulo qualquer
por biamassa00 » Sex Mai 25, 2012 22:19
- 0 Respostas
- 3589 Exibições
- Última mensagem por biamassa00

Sex Mai 25, 2012 22:19
Trigonometria
-
- Trigonometria/Triângulo
 por Pri Ferreira » Qua Mar 21, 2012 14:24
por Pri Ferreira » Qua Mar 21, 2012 14:24
- 1 Respostas
- 2119 Exibições
- Última mensagem por LuizAquino

Sáb Mar 31, 2012 14:18
Trigonometria
-
- TRIGONOMETRIA NO TRIÂNGULO RETÂNGULO
por anneliesero » Qui Set 13, 2012 18:03
- 4 Respostas
- 3295 Exibições
- Última mensagem por Cleyson007

Sex Set 14, 2012 09:36
Trigonometria
-
- TRIGONOMETRIA NO TRIÂNGULO RETÂNGULO
por anneliesero » Ter Set 18, 2012 16:54
- 1 Respostas
- 3179 Exibições
- Última mensagem por Cleyson007

Ter Set 18, 2012 17:42
Trigonometria
-
- RE: TRIGONOMETRIA NO TRIÂNGULO RETÂNGULO
por anneliesero » Ter Set 18, 2012 17:08
- 2 Respostas
- 6780 Exibições
- Última mensagem por Cleyson007

Ter Set 18, 2012 17:31
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 na figura abaixo.
na figura abaixo.




 na figura abaixo.
na figura abaixo.


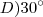




 , pois
, pois  e
e  são minhas bissetrizes externas, logo o ângulo
são minhas bissetrizes externas, logo o ângulo 

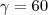
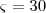



 seria construir uma cincunferência de raio
seria construir uma cincunferência de raio  desta forma observaríamos que o ponto F perntence a cincunferência, portanto,
desta forma observaríamos que o ponto F perntence a cincunferência, portanto, 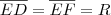 .
.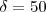


 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
