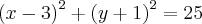verifique entre os pontos....

AjudaMatematica.com! Aqui você compartilha sua dúvida ou solução!

  • Anúncio Global
    Respostas
    Exibições
    Última mensagem

verifique entre os pontos....

Regras do fórum
Responder

verifique entre os pontos....

Mensagempor willwgo » Qua Abr 13, 2011 17:26

5-verifique entre os pontos A(0,3),B(7,2) e C(-1,3) quais pertencem a circunferencia de equação{(x-3)}^{2}+{(y+1)}^{2}=25.

me ajudem ai galara, a resposta q eu axei foi q o ponto A(0,3),B(7,2) pertencem a circunferencia mais nau tenho cereteza se está certo.
se alguem consegui faser e axar a resposta me falem como chegaram no resultado correto.
obrigado.
willwgo
Usuário Dedicado
Usuário Dedicado
 
Mensagens: 33
Registrado em: Qui Fev 17, 2011 15:59
Formação Escolar: ENSINO MÉDIO
Andamento: formado
Voltar ao topo

Re: verifique entre os pontos....

Mensagempor FilipeCaceres » Qua Abr 13, 2011 18:22

Para saber a posição de um ponto em relação a uma circunferência, basta calcular a distância do centro(C) até um ponto(P) e verificar se está é menor, maior, ou igual ao raio.
Temos 3 casos
1º)Se P é um ponto da circunferência, então d_{P,C} = r
2º)Se P é um ponto exterior à circunferência, então d_{P,C} > r
3º)Se P é um ponto interior à circunferência, então d_{P,C} < r

Sabendo que,
d_{P,C}=\sqrt{(x_p-x_c)^2+(y_p-y_c)^2}

Nesta questão o que se pede é o primeiro caso.

Obs.:
Como a equação esta escrita no forma reduzida, basta você substituir os valores de x e y de cada ponto, se o valor encontrado for 25 então o ponto pertence à circunferência.

Caso não consiga resolver poste sua dúvida.

Abraço.
FilipeCaceres
Colaborador Voluntário
Colaborador Voluntário
 
Mensagens: 351
Registrado em: Dom Out 31, 2010 21:43
Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
Área/Curso: Tec. Mecatrônica
Andamento: formado
Voltar ao topo

Re: verifique entre os pontos....

Mensagempor willwgo » Qui Abr 14, 2011 16:00

entao a resposta q axei esta certa ?!
A(0,3),B(7,2) pertencem a circunferencia.
obrigado
willwgo
Usuário Dedicado
Usuário Dedicado
 
Mensagens: 33
Registrado em: Qui Fev 17, 2011 15:59
Formação Escolar: ENSINO MÉDIO
Andamento: formado
Voltar ao topo
Responder

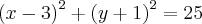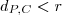
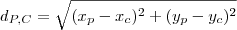
Voltar para Geometria Analítica

 


Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!

  • Tópicos relacionados
    Respostas
    Exibições
    Última mensagem

Quem está online

Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes

 


Tópico Popular

Assunto: método de contagem
Autor: sinuca147 - Seg Mai 25, 2009 09:10

Veja este exercício:

Se A = {x \in Z \hspace{1mm} | \hspace{1mm} \frac{20}{x} = n, n \in N} e B = {x \in R \hspace{1mm} | \hspace{1mm} x = 5m, m \in z}, então o número de elementos A \cap B é:

Eu tentei resolver este exercício e achei a resposta "três", mas surgiram muitas dúvidas aqui durante a resolução.

Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?

No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:

existe oposto de zero?
existe inverso de zero?
zero é par, certo?
sendo x um número natural, -x é múltiplo de x?
sendo z um número inteiro negativo, z é múltiplo de z?
sendo z um número inteiro negativo, -z é múltiplo de z?

A resposta é 3?

Obrigado.

Assunto: método de contagem
Autor: Molina - Seg Mai 25, 2009 20:42

Boa noite, sinuca.

Se A = {x \in Z \hspace{1mm} | \hspace{1mm} \frac{20}{x} = n, n \in N} você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais?
Ou seja, quais são os divisores de 20? Eles são seis: 1, 2, 4, 5, 10 e 20.
Logo, o conjunto A é A = {1, 2, 4, 5, 10, 20}

Se B = {x \in R \hspace{1mm} | \hspace{1mm} x = 5m, m \in z} você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?
Logo, o conjunto B é B = {... , -25, -20, -15, -10, -5, 0, 5, 10, 15, 20, 25, ...

Feito isso precisamos ver os números que está em ambos os conjuntos, que são: 5, 10 e 20 (3 valores, como você achou).

Vou responder rapidamente suas dúvidas porque meu tempo está estourando. Qualquer dúvida, coloque aqui, ok?

sinuca147 escreveu:No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:

existe oposto de zero? sim, é o próprio zero
existe inverso de zero? não, pois não há nenhum número que multiplicado por zero resulte em 1
zero é par, certo? sim, pois pode ser escrito da forma de 2n, onde n pertence aos inteiros
sendo x um número natural, -x é múltiplo de x? Sim, pois basta pegar x e multiplicar por -1 que encontramos -x
sendo z um número inteiro negativo, z é múltiplo de z? Sim, tais perguntando se todo número é multiplo de si mesmo
sendo z um número inteiro negativo, -z é múltiplo de z? Sim, pois basta pegar -z e multiplicar por -1 que encontramos x

A resposta é 3? Sim, pelo menos foi o que vimos a cima


Bom estudo, :y:

Assunto: método de contagem
Autor: sinuca147 - Seg Mai 25, 2009 23:35

Obrigado, mas olha só este link
http://www.colegioweb.com.br/matematica ... ro-natural
neste link encontra-se a a frase:
Múltiplo de um número natural é qualquer número que possa ser obtido multiplicando o número natural por 0, 1, 2, 3, 4, 5, etc.

Para determinarmos os múltiplos de 15, por exemplo, devemos multiplicá-lo pela sucessão dos números naturais:

Ou seja, de acordo com este link -5 não poderia ser múltiplo de 5, assim como 5 não poderia ser múltiplo de -5, eu sempre achei que não interessava o sinal na questão dos múltiplos, assim como você me confirmou, mas e essa informação contrária deste site, tem alguma credibilidade?

Há e claro, a coisa mais bacana você esqueceu, quero saber se existe algum método de contagem diferente do manual neste caso:
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?


Powered by phpBB © phpBB Group.

phpBB Mobile / SEO by Artodia.

Índice do fórum