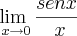 .
.Mas não consigo como neste caso por exemplo:
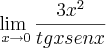

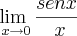 .
.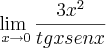

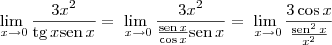


Maykids escreveu:LuizAquino ou outros amigos colaboradores, aproveitando essa deixa ai, eu posso pegar o seno que esta dividindo em baixo tipo: 1/sen x
e fazer assim 1/sen x/x ??
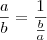 ?
?Maykids escreveu: usar o trigonometral fundamental?? no denomidador se eh que me entendem..
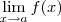 e
e 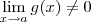 , então é válido que:
, então é válido que: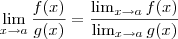
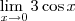 e
e 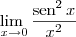 ? É verdade que
? É verdade que 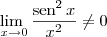 ?
?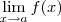 e
e 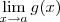 , então é válido que:
, então é válido que: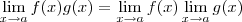



Maykids escreveu:lim1
x>0
_______
lim senx
x>0
assim entao eu axo que posso usar as propriedades fundamentais em baixo, ficando:
1
___
lim senx/x
x>0
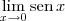 por
por 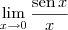 no denominador. Mas, temos que
no denominador. Mas, temos que 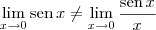 . Portanto essa substituição está errada.
. Portanto essa substituição está errada.

Maykids escreveu:lim 1/x
x>0____________
senx /x
so que ai o resultado daria 0, correto?
___________Migrando______________________-
\lim_{x>0}x^3 sen x
x³ ta indo pra zero e sen x ta indo pra zero logo o resultado dessa expressão será zero?
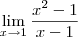 temos uma indeterminação do tipo 0/0 e o valor desse limite é 2.
temos uma indeterminação do tipo 0/0 e o valor desse limite é 2.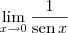 , temos uma fração com numerador constante e denominador indo para zero, o que implica que a fração vai para infinito.
, temos uma fração com numerador constante e denominador indo para zero, o que implica que a fração vai para infinito.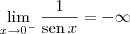
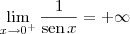

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)