![\frac{1}{1+\sqrt[n]{a}-\sqrt[n]{b}} \frac{1}{1+\sqrt[n]{a}-\sqrt[n]{b}}](/latexrender/pictures/1bbad710c53f13b1e06200df778d277c.png)
Confesso que até hoje só tive experiência com denominadores de uma
![\frac{1}{\sqrt[n]{a}} \frac{1}{\sqrt[n]{a}}](/latexrender/pictures/b9db2aa92fc98bc19e6c4692a8e8285c.png)
, mulitiplicando o numerador e o denominador pelo próprio radical sqrt[n]{a}
Ou Com duas parcelas
![\frac{1}{1+\sqrt[n]{b}} \frac{1}{1+\sqrt[n]{b}}](/latexrender/pictures/05cc4be4fe5f3d9904ca2a8c7645b27a.png) , multiplicando numerador e denomindaro pelo conjugado
, multiplicando numerador e denomindaro pelo conjugado ![1-\sqrt[n]{b} 1-\sqrt[n]{b}](/latexrender/pictures/7b446da064b249ecb4bbd1357b51a5ad.png)
1 - Tentei por:
![\sqrt[n]{a}+\sqrt[n]{b} \sqrt[n]{a}+\sqrt[n]{b}](/latexrender/pictures/eb69437975a1c14a22a6a3238a0b6f27.png)
2 - Tentei por:
![1-\sqrt[n]{a}+\sqrt[n]{b} 1-\sqrt[n]{a}+\sqrt[n]{b}](/latexrender/pictures/7dfff146747401c7896c433d3823e9eb.png)
Mas não obtive o mesmo resultado do gabarito.
Podem me ajudar.
Obrigado.
Jessé.




![\sqrt[n]{a} \sqrt[n]{a}](/latexrender/pictures/bf7ff33f3b129b15c06203d60f007807.png)
![\sqrt[n]{a^{n-1}} \sqrt[n]{a^{n-1}}](/latexrender/pictures/1d5b7d33534b20b859d6823cc6cdddfe.png) .
.![\frac{1}{\sqrt[5]{a}} = \frac{\sqrt[5]{a^4}}{\sqrt[5]{a}\sqrt[5]{a^4}} = \frac{\sqrt[5]{a^4}}{a} \frac{1}{\sqrt[5]{a}} = \frac{\sqrt[5]{a^4}}{\sqrt[5]{a}\sqrt[5]{a^4}} = \frac{\sqrt[5]{a^4}}{a}](/latexrender/pictures/a6fb4b02b4eb3cb11ace088040722f54.png)
![s = \sum_{i=0}^{n-1}(-1)^i\sqrt[n]{b^i} s = \sum_{i=0}^{n-1}(-1)^i\sqrt[n]{b^i}](/latexrender/pictures/d6379da6e42de0dc06cc7021215c95eb.png) , sendo que teremos:
, sendo que teremos:![\frac{1}{1+\sqrt[n]{b}}=
\begin{cases}
\frac{s}{1+b}\text{, se } n \text{ \'impar} \\
\frac{s}{1-b}\text{, se } n \text{ par}
\end{cases} \frac{1}{1+\sqrt[n]{b}}=
\begin{cases}
\frac{s}{1+b}\text{, se } n \text{ \'impar} \\
\frac{s}{1-b}\text{, se } n \text{ par}
\end{cases}](/latexrender/pictures/12fcd8fdc3820feaddcf2fb315657af8.png)
![\frac{1}{1+\sqrt[3]{b}} = \frac{1-\sqrt[3]{b}+\sqrt[3]{b^2}}{(1+\sqrt[3]{b})(1-\sqrt[3]{b}+\sqrt[3]{b^2})} = \frac{1-\sqrt[3]{b}+\sqrt[3]{b^2}}{1+b} \frac{1}{1+\sqrt[3]{b}} = \frac{1-\sqrt[3]{b}+\sqrt[3]{b^2}}{(1+\sqrt[3]{b})(1-\sqrt[3]{b}+\sqrt[3]{b^2})} = \frac{1-\sqrt[3]{b}+\sqrt[3]{b^2}}{1+b}](/latexrender/pictures/40501fc6d0753f81a1043027f727f35f.png)
![\frac{1}{1+\sqrt[4]{b}} = \frac{1-\sqrt[4]{b}+\sqrt[4]{b^2}-\sqrt[4]{b^3}}{(1+\sqrt[4]{b})(1-\sqrt[4]{b}+\sqrt[4]{b^2}-\sqrt[4]{b^3})} = \frac{1-\sqrt[4]{b}+\sqrt[4]{b^2}-\sqrt[4]{b^3}}{1-b} \frac{1}{1+\sqrt[4]{b}} = \frac{1-\sqrt[4]{b}+\sqrt[4]{b^2}-\sqrt[4]{b^3}}{(1+\sqrt[4]{b})(1-\sqrt[4]{b}+\sqrt[4]{b^2}-\sqrt[4]{b^3})} = \frac{1-\sqrt[4]{b}+\sqrt[4]{b^2}-\sqrt[4]{b^3}}{1-b}](/latexrender/pictures/3b39e78b6deb1e5f49672ef61b73b105.png)
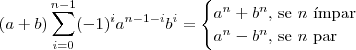
![\frac{1}{1+\sqrt[2]{2}-\sqrt[2]{3}} \frac{1}{1+\sqrt[2]{2}-\sqrt[2]{3}}](/latexrender/pictures/e86acadd0e1dcac69aefcffe19da65d4.png)
![\frac{1}{1+\sqrt{2}-\sqrt{3}} = \frac{1+\sqrt{2}+\sqrt{3}}{[(1+\sqrt{2})-\sqrt{3}][(1+\sqrt{2})+\sqrt{3}]} \frac{1}{1+\sqrt{2}-\sqrt{3}} = \frac{1+\sqrt{2}+\sqrt{3}}{[(1+\sqrt{2})-\sqrt{3}][(1+\sqrt{2})+\sqrt{3}]}](/latexrender/pictures/163a68245244d353f92abfe87db4693a.png)
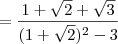
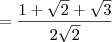
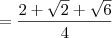
![\frac{1}{1+\sqrt[3]{2}-\sqrt[3]{3}} = \frac{(1+\sqrt[3]{2})^2 + (1+\sqrt[3]{2})\sqrt[3]{3} + \sqrt[3]{3}^2}{(1+\sqrt[3]{2}-\sqrt[3]{3})\left[(1+\sqrt[3]{2})^2 + (1+\sqrt[3]{2})\sqrt[3]{3} + \sqrt[3]{3}^2\right]} \frac{1}{1+\sqrt[3]{2}-\sqrt[3]{3}} = \frac{(1+\sqrt[3]{2})^2 + (1+\sqrt[3]{2})\sqrt[3]{3} + \sqrt[3]{3}^2}{(1+\sqrt[3]{2}-\sqrt[3]{3})\left[(1+\sqrt[3]{2})^2 + (1+\sqrt[3]{2})\sqrt[3]{3} + \sqrt[3]{3}^2\right]}](/latexrender/pictures/2c4c2492692c0c63eee0b9ac0a3c0ad1.png)
![= \frac{1+2\sqrt[3]{2}+ \sqrt[3]{3} + \sqrt[3]{4} + \sqrt[3]{6}+\sqrt[3]{9}}{(1+\sqrt[3]{2})^3-\sqrt[3]{3}^3} = \frac{1+2\sqrt[3]{2}+ \sqrt[3]{3} + \sqrt[3]{4} + \sqrt[3]{6}+\sqrt[3]{9}}{(1+\sqrt[3]{2})^3-\sqrt[3]{3}^3}](/latexrender/pictures/5991bc13e31198748eeea2931a37ec9e.png)
![= \frac{1+2\sqrt[3]{2}+ \sqrt[3]{3} + \sqrt[3]{4} + \sqrt[3]{6}+\sqrt[3]{9}}{3(\sqrt[3]{2} + \sqrt[3]{4})} = \frac{1+2\sqrt[3]{2}+ \sqrt[3]{3} + \sqrt[3]{4} + \sqrt[3]{6}+\sqrt[3]{9}}{3(\sqrt[3]{2} + \sqrt[3]{4})}](/latexrender/pictures/5fed49f3069ef8ede62436126c8eecba.png)
![= \frac{(1+2\sqrt[3]{2}+ \sqrt[3]{3} + \sqrt[3]{4} + \sqrt[3]{6}+\sqrt[3]{9})\left(\sqrt[3]{2}^2 - \sqrt[3]{2}\sqrt[3]{4} + \sqrt[3]{4}^2\right)}{3(\sqrt[3]{2} + \sqrt[3]{4})\left(\sqrt[3]{2}^2 - \sqrt[3]{2}\sqrt[3]{4} + \sqrt[3]{4}^2\right)} = \frac{(1+2\sqrt[3]{2}+ \sqrt[3]{3} + \sqrt[3]{4} + \sqrt[3]{6}+\sqrt[3]{9})\left(\sqrt[3]{2}^2 - \sqrt[3]{2}\sqrt[3]{4} + \sqrt[3]{4}^2\right)}{3(\sqrt[3]{2} + \sqrt[3]{4})\left(\sqrt[3]{2}^2 - \sqrt[3]{2}\sqrt[3]{4} + \sqrt[3]{4}^2\right)}](/latexrender/pictures/bc36d501fd3b82ac86f683ebe5996157.png)
![= \frac{6 + 3\sqrt[3]{4} - 2\sqrt[3]{9} + 3\sqrt[3]{12} + 2\sqrt[3]{18} + \sqrt[3]{36}}{3\left(\sqrt[3]{2}^3 + \sqrt[3]{4}^3\right)} = \frac{6 + 3\sqrt[3]{4} - 2\sqrt[3]{9} + 3\sqrt[3]{12} + 2\sqrt[3]{18} + \sqrt[3]{36}}{3\left(\sqrt[3]{2}^3 + \sqrt[3]{4}^3\right)}](/latexrender/pictures/b75824f2d5834cd4ca7a36a897464690.png)
![= \frac{6 + 3\sqrt[3]{4} - 2\sqrt[3]{9} + 3\sqrt[3]{12} + 2\sqrt[3]{18} + \sqrt[3]{36}}{18} = \frac{6 + 3\sqrt[3]{4} - 2\sqrt[3]{9} + 3\sqrt[3]{12} + 2\sqrt[3]{18} + \sqrt[3]{36}}{18}](/latexrender/pictures/906fecd38f38ec8efa038dc2d9bdead8.png)

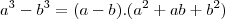
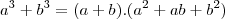

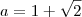
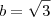
 e só falta
e só falta  e por coencidência é o próprio conjudado, desta forma não é so trocar o sinal como já foi dito.
e por coencidência é o próprio conjudado, desta forma não é so trocar o sinal como já foi dito.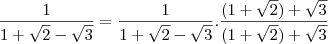 daqui em diante a solução é igual.
daqui em diante a solução é igual.![\frac{1}{1+\sqrt[3]{2}-\sqrt[3]{3}} \frac{1}{1+\sqrt[3]{2}-\sqrt[3]{3}}](/latexrender/pictures/eeb3af157f857af975b4483a03d5c052.png)
![a=1+\sqrt[3]{2} a=1+\sqrt[3]{2}](/latexrender/pictures/b4bfb953bd9ee57f351b34f99bcbccda.png)
![b=\sqrt[3]{3}} b=\sqrt[3]{3}}](/latexrender/pictures/7d73c21ea353b8c30acda90e803c0004.png)
 .
. então o que nos falta é
então o que nos falta é 
![\frac{1}{1+\sqrt[3]{2}-\sqrt[3]{3}} = \frac{1}{1+\sqrt[3]{2}-\sqrt[3]{3}}.\frac{(1+\sqrt[3]{2})^2 + (1+\sqrt[3]{2})\sqrt[3]{3} + \sqrt[3]{3}^2}{(1+\sqrt[3]{2})^2 + (1+\sqrt[3]{2})\sqrt[3]{3} + \sqrt[3]{3}^2\right} \frac{1}{1+\sqrt[3]{2}-\sqrt[3]{3}} = \frac{1}{1+\sqrt[3]{2}-\sqrt[3]{3}}.\frac{(1+\sqrt[3]{2})^2 + (1+\sqrt[3]{2})\sqrt[3]{3} + \sqrt[3]{3}^2}{(1+\sqrt[3]{2})^2 + (1+\sqrt[3]{2})\sqrt[3]{3} + \sqrt[3]{3}^2\right}](/latexrender/pictures/bc28700e3690dd26f75999699772ef32.png) daqui segue igual.
daqui segue igual.
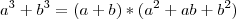 . Creio que houve alguma falha na sua digitação.
. Creio que houve alguma falha na sua digitação.
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.