 por 380625 » Sex Abr 01, 2011 15:58
por 380625 » Sex Abr 01, 2011 15:58
Boa tarde estou no primeiro ano de graduação e estou tendo a materia Geometria Analitica o professor esta definindo segmento orientado e vetor. Mas para definir isso precisamos saber o que é equipolencia. Entre as definições esta tudo bem entendi bem o que sao segmentos orientados, classe de equipolência e vetores. Porem, não consigo provar e desenhar algumas coisas por exemplo:
1 - (A,B)~(C,D) IMPLICA (A,C)~(B,D) no livro em que estudo ele vez um caso particular dessa proposição no caso em que o quadrilatero ABCD é um paralelog
Após isso ele me faz tres questoes
Faça um desenho ilustrando a proposição 1 em que ABCD sao colineares.
Prove que (A,B)~(C,D) IMPLICA (B,A)~(D,C)
Prove que (A,B)~(C,D) IMPLICA (C,A)~(D,B).
Gostaria de dicas pois sei que é meio abstraro algumas coisas ainda mais quando estamos começando G.A.
Grato Flávio Santana
-
380625
- Usuário Dedicado

-
- Mensagens: 48
- Registrado em: Sex Fev 18, 2011 17:38
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física
- Andamento: cursando
 por LuizAquino » Sex Abr 01, 2011 17:25
por LuizAquino » Sex Abr 01, 2011 17:25
Dicas380625 escreveu:Faça um desenho ilustrando a proposição 1 em que ABCD sao colineares.
Lembre-se que "colineares" significa que os pontos estão sobre uma mesma reta.
380625 escreveu:Prove que (A,B)~(C,D) IMPLICA (B,A)~(D,C)
Lembre-se que (A, B) é um segmento orientado com mesma direção, magnitude e sentido contrário a (B, A).
380625 escreveu:Prove que (A,B)~(C,D) IMPLICA (C,A)~(D,B).
Lembre-se do paralelogramo ABCD.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por 0 kelvin » Sáb Abr 02, 2011 00:10
por 0 kelvin » Sáb Abr 02, 2011 00:10
Estou recebendo esses mesmos exercícios para resolver

Do que entendi por enquanto foi que precisa prestar atenção na definição que tem no livro, mas não apenas na descrição, principalmente na parte que utiliza os símbolos, a notação matemática dos vetores.
Tambem senti que vetores são abstratos, talvez fiquem mais claros quando começarem a ser usados na física mesmo.
-
0 kelvin
- Usuário Parceiro

-
- Mensagens: 78
- Registrado em: Dom Out 31, 2010 16:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciencias atmosfericas
- Andamento: cursando
 por MarceloFantini » Sáb Abr 02, 2011 01:04
por MarceloFantini » Sáb Abr 02, 2011 01:04
Vetores ficarão mais claros quando estudarem Álgebra Linear. Quanto antes vocês destituírem-se da idéia de vetor como apenas uma flecha, melhor.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por 380625 » Dom Abr 03, 2011 12:32
por 380625 » Dom Abr 03, 2011 12:32
Esse exercicio eu consegui resolver:
Prove que (A,B)~(P,Q) e (C,D)~(P,Q) IMPLICA (A,B)~(C,D):
No exercicio acima eu usei a propriedade simetrica e depois a transitiva e consegui resolver.
Então o que ta dificil para mim é:
Prove que (A,B)~(C,D)~IMPLICA(B,A)~(D,C), pois não consigo relacionar esse exercicio com as propriedades simetrica e transitiva.
Flávio Santana.
-
380625
- Usuário Dedicado

-
- Mensagens: 48
- Registrado em: Sex Fev 18, 2011 17:38
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física
- Andamento: cursando
 por LuizAquino » Dom Abr 03, 2011 12:55
por LuizAquino » Dom Abr 03, 2011 12:55
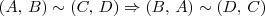
Temos que (A, B) e (C, D) são tais que possuem:
- magnitude: m
- direção: d
- sentido: s
Sabemos que (B, A) possui:
- magnitude: m
- direção: d
- sentido: -s (isto é, o sentido contrário de (A, B)).
Além disso, sabemos que (D, C) possui:
- magnitude: m
- direção: d
- sentido: -s (isto é, o sentido contrário de (C, D)).
Portanto, (B, A) e (D, C) são equipolentes.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Geometria Analitica (Graduação).
por 380625 » Ter Mar 29, 2011 11:44
- 1 Respostas
- 1037 Exibições
- Última mensagem por LuizAquino

Ter Mar 29, 2011 12:05
Geometria Analítica
-
- Geometria Analitica (Graduação).
por 380625 » Seg Abr 18, 2011 17:26
- 1 Respostas
- 997 Exibições
- Última mensagem por LuizAquino

Seg Abr 18, 2011 19:59
Geometria Analítica
-
- Questão CEFET-MG graduação 2012
por Thulio_Parazi » Qui Abr 05, 2012 11:24
- 1 Respostas
- 2131 Exibições
- Última mensagem por fraol

Sex Abr 06, 2012 20:54
Trigonometria
-
- Geometria Analítica
por maysa » Ter Abr 14, 2009 10:35
- 1 Respostas
- 7688 Exibições
- Última mensagem por Marcampucio

Ter Abr 14, 2009 15:52
Geometria Analítica
-
- GEOMETRIA ANALITICA
por GABRIELA » Ter Set 29, 2009 17:20
- 3 Respostas
- 5449 Exibições
- Última mensagem por GABRIELA

Qua Set 30, 2009 16:49
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.






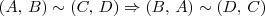


 , avisa que eu resolvo.
, avisa que eu resolvo.

