 por valeuleo » Qui Mar 31, 2011 08:46
por valeuleo » Qui Mar 31, 2011 08:46
Já tentei usar todas as regras demonstradas pelo professor mas não estou conseguindo chegar ao fim deste problema. Alguém pode me ajudar? Grato
![\lim_{x\to1} \frac{\sqrt[4]{x} + \sqrt[3]{x} + \sqrt[]{x} - 3} {x - 1} \lim_{x\to1} \frac{\sqrt[4]{x} + \sqrt[3]{x} + \sqrt[]{x} - 3} {x - 1}](/latexrender/pictures/402eea40a69caf6457f3a3539e033709.png)
O método que o Prof. quer que usemos é o de mudança de variável, onde cálculamos o m.m.c dos índices dos radicais.
-
valeuleo
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Qua Mar 23, 2011 14:19
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciências da Computação
- Andamento: cursando
 por LuizAquino » Qui Mar 31, 2011 10:44
por LuizAquino » Qui Mar 31, 2011 10:44
Fazendo a substituição
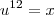
, temos que:
![\lim_{x\to1} \frac{\sqrt[4]{x} + \sqrt[3]{x} + \sqrt[]{x} - 3} {x - 1} \Rightarrow \lim_{u \to 1} \frac{u^6 + u^4 + u^3 - 3} {u^{12} - 1} \lim_{x\to1} \frac{\sqrt[4]{x} + \sqrt[3]{x} + \sqrt[]{x} - 3} {x - 1} \Rightarrow \lim_{u \to 1} \frac{u^6 + u^4 + u^3 - 3} {u^{12} - 1}](/latexrender/pictures/caba58eb550e958fd80f889fc574c5da.png)
Provavelmente, a sua dificuldade está em realizar a divisão entre os polinômios. Recomendo que estude o assunto [1, 2].
Nesse caso, a divisão de

por u-1 resulta em quociente
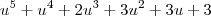
e resto 0. Ou seja, temos que:

Agora, tente terminar o exercício.
Referência
[1]
Divisão de polinômios - Brasil Escola -
http://www.brasilescola.com/matematica/ ... nomios.htm[2]
Briot Ruffini -
http://www.youtube.com/watch?v=yv5ju6Q81dMEditado pela última vez por
LuizAquino em Qui Mar 31, 2011 11:43, em um total de 3 vezes.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por valeuleo » Qui Mar 31, 2011 11:18
por valeuleo » Qui Mar 31, 2011 11:18
Na verdade não é pra desenvolver a divisão, mas sim obter o valor. A resposta é
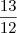
, mas ainda não consegui resolver.
-
valeuleo
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Qua Mar 23, 2011 14:19
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciências da Computação
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- LIMITE COM RADICAIS como fatorar ou simplificar
por pedroklein+1978 » Ter Abr 25, 2017 18:42
- 0 Respostas
- 2864 Exibições
- Última mensagem por pedroklein+1978

Ter Abr 25, 2017 18:42
Cálculo: Limites, Derivadas e Integrais
-
- Radicais
por agfp5 » Sáb Out 30, 2010 08:50
- 2 Respostas
- 2334 Exibições
- Última mensagem por agfp5

Sáb Out 30, 2010 09:10
Geometria Plana
-
- Radicais
por Andrewo » Qua Fev 01, 2012 13:43
- 8 Respostas
- 4123 Exibições
- Última mensagem por LuizAquino

Qua Fev 08, 2012 12:22
Álgebra Elementar
-
- Radicais II
por Andrewo » Qui Fev 09, 2012 19:38
- 3 Respostas
- 1877 Exibições
- Última mensagem por MarceloFantini

Sex Fev 10, 2012 11:32
Álgebra Elementar
-
- Radicais de nv
por Andrewo » Seg Fev 13, 2012 16:58
- 4 Respostas
- 2456 Exibições
- Última mensagem por Arkanus Darondra

Ter Fev 14, 2012 13:01
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\lim_{x\to1} \frac{\sqrt[4]{x} + \sqrt[3]{x} + \sqrt[]{x} - 3} {x - 1} \lim_{x\to1} \frac{\sqrt[4]{x} + \sqrt[3]{x} + \sqrt[]{x} - 3} {x - 1}](/latexrender/pictures/402eea40a69caf6457f3a3539e033709.png)

![\lim_{x\to1} \frac{\sqrt[4]{x} + \sqrt[3]{x} + \sqrt[]{x} - 3} {x - 1} \lim_{x\to1} \frac{\sqrt[4]{x} + \sqrt[3]{x} + \sqrt[]{x} - 3} {x - 1}](/latexrender/pictures/402eea40a69caf6457f3a3539e033709.png)

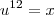 , temos que:
, temos que:![\lim_{x\to1} \frac{\sqrt[4]{x} + \sqrt[3]{x} + \sqrt[]{x} - 3} {x - 1} \Rightarrow \lim_{u \to 1} \frac{u^6 + u^4 + u^3 - 3} {u^{12} - 1} \lim_{x\to1} \frac{\sqrt[4]{x} + \sqrt[3]{x} + \sqrt[]{x} - 3} {x - 1} \Rightarrow \lim_{u \to 1} \frac{u^6 + u^4 + u^3 - 3} {u^{12} - 1}](/latexrender/pictures/caba58eb550e958fd80f889fc574c5da.png)
 por u-1 resulta em quociente
por u-1 resulta em quociente 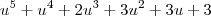 e resto 0. Ou seja, temos que:
e resto 0. Ou seja, temos que:

, temos que:
e resto 0. Ou seja, temos que:
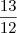 , mas ainda não consegui resolver.
, mas ainda não consegui resolver.
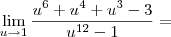

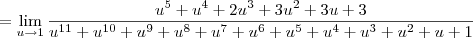
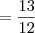



 , avisa que eu resolvo.
, avisa que eu resolvo.

