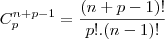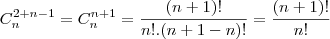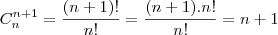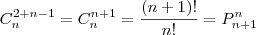0.
0.a) Calcule de quantas maneiras distintas n bolas idênticas podem ser distribuídas entre Luís e Antônio.
b) Calcule de quantas maneiras distintas n bolas idênticas podem ser distribuídas entre Pedro,Luís e Antônio.
Por favor, quem for resolver me explique o porquê do ( n+1) .... que foi o q eu não entendi..
Obrigada !


 , onde
, onde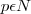 (N = conjunto dos números naturais).
(N = conjunto dos números naturais).