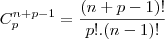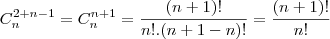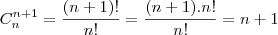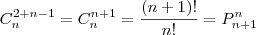por my2009 » Qua Mar 30, 2011 10:00
por my2009 » Qua Mar 30, 2011 10:00
Seja n um número inteiro, n

0.
a) Calcule de quantas maneiras distintas n bolas idênticas podem ser distribuídas entre Luís e Antônio.
b) Calcule de quantas maneiras distintas n bolas idênticas podem ser distribuídas entre Pedro,Luís e Antônio.
Por favor, quem for resolver me explique o porquê do ( n+1) .... que foi o q eu não entendi..
Obrigada !
-
my2009
- Colaborador Voluntário

-
- Mensagens: 104
- Registrado em: Seg Mai 24, 2010 13:57
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por FilipeCaceres » Qua Mar 30, 2011 10:31
por FilipeCaceres » Qua Mar 30, 2011 10:31
Oi My,
Procure por número de soluções inteiras e não negativas de uma equação linear para obter mais informações e aprender como se resolve esses tipos de questões.
Ex.:
Considere a equação linear a seguir:

, onde
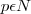
(N = conjunto dos números naturais).
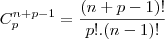
Voltando para a questão.
A) Seja x o número de bolas recebidas por Luís e y o número de bolas recebidas por Antônio. Do enunciado temos a equação x + y = n.
Logo temos,
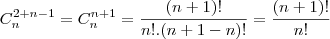
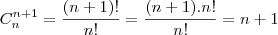

B)Sendo z o número de bolas recebidas por Pedro, temos a equação x + y + z = n.
Use o mesmo raciocínio anterior e tente fazer esta, qualquer dúvida pergunte.
Espero ter ajudado.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por my2009 » Qua Mar 30, 2011 10:38
por my2009 » Qua Mar 30, 2011 10:38
Olá Felipe, tudo bem com vc?
Então.. ainda não entendi... pq ( n+1 ) ?
aqui na resolução Ele utiliza P ao invés de C .... poderia tmb utlizar a permutação para resolver essa questão ?
-
my2009
- Colaborador Voluntário

-
- Mensagens: 104
- Registrado em: Seg Mai 24, 2010 13:57
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por my2009 » Qua Mar 30, 2011 10:40
por my2009 » Qua Mar 30, 2011 10:40
rsrsrsrs ha ta ja entendi... =p

obrigada
-
my2009
- Colaborador Voluntário

-
- Mensagens: 104
- Registrado em: Seg Mai 24, 2010 13:57
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por FilipeCaceres » Qua Mar 30, 2011 11:18
por FilipeCaceres » Qua Mar 30, 2011 11:18
Que bom que você entendeu, mas só para complementar, poderia ser utilizado permutação sem problema nenhum, observe que:
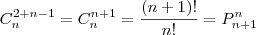
Abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
Voltar para Estatística
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Questão da Fuvest
por Kelvin Brayan » Qua Mar 02, 2011 11:56
- 2 Respostas
- 4131 Exibições
- Última mensagem por Kelvin Brayan

Qua Mar 02, 2011 13:23
Álgebra Elementar
-
- Questão Fuvest
 por Alex Rom » Qua Mar 30, 2011 11:38
por Alex Rom » Qua Mar 30, 2011 11:38
- 2 Respostas
- 3622 Exibições
- Última mensagem por Alex Rom

Qua Mar 30, 2011 12:07
Geometria Plana
-
- Questão da Fuvest
 por Kelvin Brayan » Seg Abr 18, 2011 17:11
por Kelvin Brayan » Seg Abr 18, 2011 17:11
- 2 Respostas
- 1720 Exibições
- Última mensagem por Kelvin Brayan

Ter Abr 19, 2011 12:57
Álgebra Elementar
-
- Questão FUVEST
por Guilherme Carvalho » Ter Mai 10, 2011 17:19
- 5 Respostas
- 2876 Exibições
- Última mensagem por carlosalesouza

Sex Mai 13, 2011 15:50
Logaritmos
-
- Questão FUVEST
por LuRodrigues » Seg Abr 23, 2012 13:26
- 1 Respostas
- 1214 Exibições
- Última mensagem por Fabiano Vieira

Seg Abr 23, 2012 19:30
Matemática Financeira
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 0.
0.

 , onde
, onde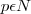 (N = conjunto dos números naturais).
(N = conjunto dos números naturais).