Olá amigos, estou resolvendo algumas questões sobre funções, mas eu me deparei com esta questão abaixo que me deixou na dúvida :
(UECE) Seja f: R -> R a função tal que f(1) = 4 e f(x+1) = 4 f(x) para todo real. Nessas condições, f(10) é igual a ?
O que me deixou na dúvida foi justamente isso f(x+1) = 4 f(x), pois não sei calcular a f(10), se x=10 ou se x+1 será = 10.
Ajudem-me por favor !
Obrigado !
Resposta do gabarito : f(10) = 1024


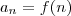 .
. .
.
 .
. = f(n) e
= f(n) e  então: q=4
então: q=4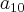 e
e  temos:
temos: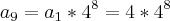 =>
=> 
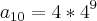 =
= 

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)