 por Kelvin Brayan » Dom Mar 27, 2011 13:26
por Kelvin Brayan » Dom Mar 27, 2011 13:26
Olá amigos, estou resolvendo algumas questões sobre funções, mas eu me deparei com esta questão abaixo que me deixou na dúvida :
(UECE) Seja f: R -> R a função tal que f(1) = 4 e f(x+1) = 4 f(x) para todo real. Nessas condições, f(10) é igual a ?
O que me deixou na dúvida foi justamente isso f(x+1) = 4 f(x), pois não sei calcular a f(10), se x=10 ou se x+1 será = 10.
Ajudem-me por favor !
Obrigado !
Resposta do gabarito : f(10) = 1024
-
Kelvin Brayan
- Colaborador Voluntário

-
- Mensagens: 111
- Registrado em: Dom Fev 20, 2011 16:50
- Localização: Varginha - MG
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Inglês
- Andamento: cursando
 por LuizAquino » Dom Mar 27, 2011 13:39
por LuizAquino » Dom Mar 27, 2011 13:39
DicaConsidere a sequência com termo geral
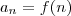
.
Note que essa sequência será tal que

.
Pergunta: que tipo de sequência é formada quando cada termo é igual ao termo anterior multiplicado por uma constante?
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Kelvin Brayan » Dom Mar 27, 2011 13:42
por Kelvin Brayan » Dom Mar 27, 2011 13:42
PG?
-
Kelvin Brayan
- Colaborador Voluntário

-
- Mensagens: 111
- Registrado em: Dom Fev 20, 2011 16:50
- Localização: Varginha - MG
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Inglês
- Andamento: cursando
 por LuizAquino » Dom Mar 27, 2011 13:48
por LuizAquino » Dom Mar 27, 2011 13:48
Exato! Essa sequência forma uma p.g..
Aproveito para dizer-lhe que você deve rever o gabarito, pois o que você indicou não está correto.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Kelvin Brayan » Dom Mar 27, 2011 13:52
por Kelvin Brayan » Dom Mar 27, 2011 13:52
Opa! mil desculpas a resposta é

.
Muito Obrigado ! Vou tentar resolvê-la agora !
-
Kelvin Brayan
- Colaborador Voluntário

-
- Mensagens: 111
- Registrado em: Dom Fev 20, 2011 16:50
- Localização: Varginha - MG
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Inglês
- Andamento: cursando
 por Kelvin Brayan » Dom Mar 27, 2011 14:08
por Kelvin Brayan » Dom Mar 27, 2011 14:08
Luiz Aquino, veja se fiz corretamente:
Se

= f(n) e

então: q=4
f(10) =
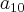
e

temos:
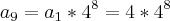
=>

Por fim :
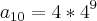
=

.
Certo? essa era a única maneira de resolver tal questão? porque nem aprendi direio PA E PG ainda no cursinho, mas lembro disso no ensino médio !
-
Kelvin Brayan
- Colaborador Voluntário

-
- Mensagens: 111
- Registrado em: Dom Fev 20, 2011 16:50
- Localização: Varginha - MG
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Inglês
- Andamento: cursando
 por LuizAquino » Dom Mar 27, 2011 14:35
por LuizAquino » Dom Mar 27, 2011 14:35
A forma mais simples de resolver é aplicando os conceitos de p.g..
Uma outra forma de resolução, mais trabalhosa, seria desenvolver para alguns termos e tentar "enxergar" o padrão:
f(1)=4
f(2)=4f(1)=4^2
f(3)=4f(2)=4^3
f(4)=4f(3)=4^4
f(5)=4f(4)=4^5
(...)
f(10)=4f(9)=4^10
Note que de qualquer modo acaba aparecendo o conceito de p.g..
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Kelvin Brayan » Dom Mar 27, 2011 15:20
por Kelvin Brayan » Dom Mar 27, 2011 15:20
Obrigado mais uma vez !
-
Kelvin Brayan
- Colaborador Voluntário

-
- Mensagens: 111
- Registrado em: Dom Fev 20, 2011 16:50
- Localização: Varginha - MG
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Inglês
- Andamento: cursando
 por profmatematica » Dom Mar 27, 2011 16:56
por profmatematica » Dom Mar 27, 2011 16:56
X+1=1 ok? Entao X=0 seguindo faremos f(2)=4*f(1) entao f(2)=4*4= 4^2 seguindo f(3)=4*f(2) logo f(3)=4*4^2=4^3 entao seguindo temos que f(10)=4^10
Editado pela última vez por
profmatematica em Dom Mar 27, 2011 17:13, em um total de 1 vez.
-
profmatematica
- Usuário Dedicado

-
- Mensagens: 42
- Registrado em: Sex Ago 27, 2010 13:34
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
 por Kelvin Brayan » Dom Mar 27, 2011 17:02
por Kelvin Brayan » Dom Mar 27, 2011 17:02
Valeu !
-
Kelvin Brayan
- Colaborador Voluntário

-
- Mensagens: 111
- Registrado em: Dom Fev 20, 2011 16:50
- Localização: Varginha - MG
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Inglês
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Questão da UECE
por vini15963 » Seg Set 22, 2014 01:25
- 0 Respostas
- 3605 Exibições
- Última mensagem por vini15963

Seg Set 22, 2014 01:25
Geometria Espacial
-
- Questão UECE 2012
por Phaniemor » Qui Abr 18, 2013 11:33
- 1 Respostas
- 4481 Exibições
- Última mensagem por DanielFerreira

Qui Abr 18, 2013 12:01
Binômio de Newton
-
- [Cilindro e Esfera] Questão de vestibular UECE relação
por gustavoluiss » Seg Jan 09, 2012 21:46
- 1 Respostas
- 4217 Exibições
- Última mensagem por ant_dii

Ter Jan 10, 2012 02:08
Geometria Espacial
-
- Piramide UECE
por Maria Livia » Sex Nov 16, 2012 11:45
- 1 Respostas
- 9397 Exibições
- Última mensagem por young_jedi

Sex Nov 16, 2012 12:23
Geometria Espacial
-
- Logarítmos UECE
por Amanda185 » Qua Mai 22, 2013 15:37
- 2 Respostas
- 5999 Exibições
- Última mensagem por nicholasrr

Qui Abr 03, 2014 21:30
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


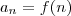 .
. .
.
 .
. = f(n) e
= f(n) e  então: q=4
então: q=4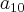 e
e  temos:
temos: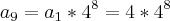 =>
=> 
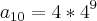 =
= 

