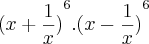
aquele ponto entre os parenteses e sinal de multiplicação
e tbm o grande responsavel pela dificuldade da questão!!
OBS:caros voluntarios ou responsaveis pelo site caso consigam resolver isso prometo que ficarei um bom tempo sem perguntar a vcs kkkk!! desde ja agradeço!!


 .
. .
. .
.
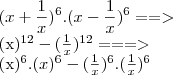
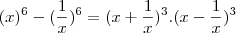
 ===>
===>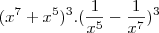
![{\left(x+\frac{1}{x}\right)}^{6}.{\left(x-\frac{1}{x}\right)}^{6} = \left[\left(x+\frac{1}{x}\right)\left(x-\frac{1}{x}\right)\right]^6 {\left(x+\frac{1}{x}\right)}^{6}.{\left(x-\frac{1}{x}\right)}^{6} = \left[\left(x+\frac{1}{x}\right)\left(x-\frac{1}{x}\right)\right]^6](/latexrender/pictures/32b426e082ed4bee4b3e89a478cc78c4.png)
![\left[\left(x+\frac{1}{x}\right)\left(x-\frac{1}{x}\right)\right]^6 = \left(x^2-\frac{1}{x^2}\right)^6 \left[\left(x+\frac{1}{x}\right)\left(x-\frac{1}{x}\right)\right]^6 = \left(x^2-\frac{1}{x^2}\right)^6](/latexrender/pictures/2f80613dfd5a938a5b38eb73954e1c7e.png)
![\left[x^2+\left(-\frac{1}{x^2}\right)\right]^6 = \sum_{i=0}^{6} {6 \choose i} \left(x^2\right)^{6-i}\left(-\frac{1}{x^2}\right)^{i} \left[x^2+\left(-\frac{1}{x^2}\right)\right]^6 = \sum_{i=0}^{6} {6 \choose i} \left(x^2\right)^{6-i}\left(-\frac{1}{x^2}\right)^{i}](/latexrender/pictures/2443b5dd63030510c20e3122227ecbf8.png)
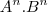 , isso é igual a
, isso é igual a 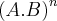 portanto :
portanto : ![{(x + \frac{1}{x})}^{6} . {(x - \frac{1}{x})}^{6} = {[(x + \frac{1}{x}). (x + \frac{1}{x})]}^{6} = ({x}^{2} - \frac{1}{{x}^{2}})^{6} {(x + \frac{1}{x})}^{6} . {(x - \frac{1}{x})}^{6} = {[(x + \frac{1}{x}). (x + \frac{1}{x})]}^{6} = ({x}^{2} - \frac{1}{{x}^{2}})^{6}](/latexrender/pictures/a40b2064d93805879bf0efd6abd848d6.png)

 para encontrar o termo independente temos, desprezando as bases:
para encontrar o termo independente temos, desprezando as bases:
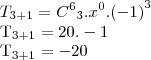

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)