 por Fabricio dalla » Ter Mar 15, 2011 15:21
por Fabricio dalla » Ter Mar 15, 2011 15:21
calcule o termo independente de x no desenvolvimento de:
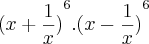
aquele ponto entre os parenteses e sinal de multiplicação
e tbm o grande responsavel pela dificuldade da questão!!
OBS:caros voluntarios ou responsaveis pelo site caso consigam resolver isso prometo que ficarei um bom tempo sem perguntar a vcs kkkk!! desde ja agradeço!!
-
Fabricio dalla
- Colaborador Voluntário

-
- Mensagens: 111
- Registrado em: Sáb Fev 26, 2011 17:50
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por LuizAquino » Ter Mar 15, 2011 18:46
por LuizAquino » Ter Mar 15, 2011 18:46
Dicas(i) Lembre-se da propriedade de potenciação:

.
(ii) Lembre-se do produto notável:

.
(iii) Lembre-se do binômio de Newton:
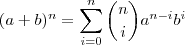
.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Fabricio dalla » Sáb Mar 19, 2011 18:45
por Fabricio dalla » Sáb Mar 19, 2011 18:45
Tá no desenvolvimento meu que provavelmente ta errado fico:
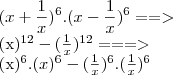
onde:
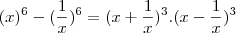
tem-se:

===>
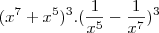
ta, se ta certo ou nao morri aqui!. Dá uma luz ai LuizAquino ou qualquer outro voluntario
-
Fabricio dalla
- Colaborador Voluntário

-
- Mensagens: 111
- Registrado em: Sáb Fev 26, 2011 17:50
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por LuizAquino » Sáb Mar 19, 2011 19:24
por LuizAquino » Sáb Mar 19, 2011 19:24
As dicas que dei são mais do que suficientes!
(i) Lembre-se da propriedade de potenciação:

.
![{\left(x+\frac{1}{x}\right)}^{6}.{\left(x-\frac{1}{x}\right)}^{6} = \left[\left(x+\frac{1}{x}\right)\left(x-\frac{1}{x}\right)\right]^6 {\left(x+\frac{1}{x}\right)}^{6}.{\left(x-\frac{1}{x}\right)}^{6} = \left[\left(x+\frac{1}{x}\right)\left(x-\frac{1}{x}\right)\right]^6](/latexrender/pictures/32b426e082ed4bee4b3e89a478cc78c4.png)
(ii) Lembre-se do produto notável:

.
![\left[\left(x+\frac{1}{x}\right)\left(x-\frac{1}{x}\right)\right]^6 = \left(x^2-\frac{1}{x^2}\right)^6 \left[\left(x+\frac{1}{x}\right)\left(x-\frac{1}{x}\right)\right]^6 = \left(x^2-\frac{1}{x^2}\right)^6](/latexrender/pictures/2f80613dfd5a938a5b38eb73954e1c7e.png)
(iii) Lembre-se do binômio de Newton:
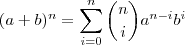
.
![\left[x^2+\left(-\frac{1}{x^2}\right)\right]^6 = \sum_{i=0}^{6} {6 \choose i} \left(x^2\right)^{6-i}\left(-\frac{1}{x^2}\right)^{i} \left[x^2+\left(-\frac{1}{x^2}\right)\right]^6 = \sum_{i=0}^{6} {6 \choose i} \left(x^2\right)^{6-i}\left(-\frac{1}{x^2}\right)^{i}](/latexrender/pictures/2443b5dd63030510c20e3122227ecbf8.png)
Agora você tem que ser capaz de terminar a questão.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Pedro123 » Sáb Mar 19, 2011 19:39
por Pedro123 » Sáb Mar 19, 2011 19:39
Fabricio, faça o seguinte, lembre que se temos:
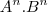
, isso é igual a
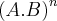
portanto :
![{(x + \frac{1}{x})}^{6} . {(x - \frac{1}{x})}^{6} = {[(x + \frac{1}{x}). (x + \frac{1}{x})]}^{6} = ({x}^{2} - \frac{1}{{x}^{2}})^{6} {(x + \frac{1}{x})}^{6} . {(x - \frac{1}{x})}^{6} = {[(x + \frac{1}{x}). (x + \frac{1}{x})]}^{6} = ({x}^{2} - \frac{1}{{x}^{2}})^{6}](/latexrender/pictures/a40b2064d93805879bf0efd6abd848d6.png)
agora utilizando as propriedades de Binômio de Newton:

fazendo

para encontrar o termo independente temos, desprezando as bases:

agora na parte final :
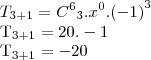
-
Pedro123
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Qui Jun 10, 2010 22:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecanica - 1° Período
- Andamento: cursando
 por Fabricio dalla » Sáb Mar 19, 2011 20:38
por Fabricio dalla » Sáb Mar 19, 2011 20:38
è LuizAquino concordo com vc, errar produto notavel é inadmissivel :/
-
Fabricio dalla
- Colaborador Voluntário

-
- Mensagens: 111
- Registrado em: Sáb Fev 26, 2011 17:50
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Binômio de Newton
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Limites, uma mãozinha aqui
por D_Honda » Qui Jan 07, 2010 23:22
- 2 Respostas
- 4325 Exibições
- Última mensagem por D_Honda

Sex Jan 08, 2010 19:49
Cálculo: Limites, Derivadas e Integrais
-
- Preciso de ajuda com esse exercício
por Dankaerte » Qui Set 10, 2009 19:10
- 2 Respostas
- 6293 Exibições
- Última mensagem por Elcioschin

Ter Abr 13, 2010 14:01
Matrizes e Determinantes
-
- Preciso da Resolução desse exercicio
por alexcaju » Sex Jan 17, 2014 19:58
- 0 Respostas
- 1069 Exibições
- Última mensagem por alexcaju

Sex Jan 17, 2014 19:58
Matemática Financeira
-
- Boa tarde preciso de uma orientação neste exercicio
por valdinei » Qua Nov 16, 2016 18:19
- 1 Respostas
- 3630 Exibições
- Última mensagem por adauto martins

Sex Nov 18, 2016 16:41
Cálculo: Limites, Derivadas e Integrais
-
- Preciso saber a fórmula para resolver esse exercício
por Dankaerte » Qui Ago 27, 2009 14:19
- 1 Respostas
- 6967 Exibições
- Última mensagem por Molina

Qui Ago 27, 2009 14:58
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
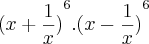


 .
. .
.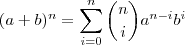 .
.
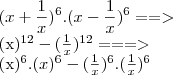
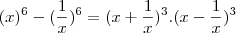
 ===>
===>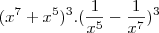
![{\left(x+\frac{1}{x}\right)}^{6}.{\left(x-\frac{1}{x}\right)}^{6} = \left[\left(x+\frac{1}{x}\right)\left(x-\frac{1}{x}\right)\right]^6 {\left(x+\frac{1}{x}\right)}^{6}.{\left(x-\frac{1}{x}\right)}^{6} = \left[\left(x+\frac{1}{x}\right)\left(x-\frac{1}{x}\right)\right]^6](/latexrender/pictures/32b426e082ed4bee4b3e89a478cc78c4.png)
![\left[\left(x+\frac{1}{x}\right)\left(x-\frac{1}{x}\right)\right]^6 = \left(x^2-\frac{1}{x^2}\right)^6 \left[\left(x+\frac{1}{x}\right)\left(x-\frac{1}{x}\right)\right]^6 = \left(x^2-\frac{1}{x^2}\right)^6](/latexrender/pictures/2f80613dfd5a938a5b38eb73954e1c7e.png)
![\left[x^2+\left(-\frac{1}{x^2}\right)\right]^6 = \sum_{i=0}^{6} {6 \choose i} \left(x^2\right)^{6-i}\left(-\frac{1}{x^2}\right)^{i} \left[x^2+\left(-\frac{1}{x^2}\right)\right]^6 = \sum_{i=0}^{6} {6 \choose i} \left(x^2\right)^{6-i}\left(-\frac{1}{x^2}\right)^{i}](/latexrender/pictures/2443b5dd63030510c20e3122227ecbf8.png)
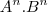 , isso é igual a
, isso é igual a 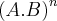 portanto :
portanto : ![{(x + \frac{1}{x})}^{6} . {(x - \frac{1}{x})}^{6} = {[(x + \frac{1}{x}). (x + \frac{1}{x})]}^{6} = ({x}^{2} - \frac{1}{{x}^{2}})^{6} {(x + \frac{1}{x})}^{6} . {(x - \frac{1}{x})}^{6} = {[(x + \frac{1}{x}). (x + \frac{1}{x})]}^{6} = ({x}^{2} - \frac{1}{{x}^{2}})^{6}](/latexrender/pictures/a40b2064d93805879bf0efd6abd848d6.png)

 para encontrar o termo independente temos, desprezando as bases:
para encontrar o termo independente temos, desprezando as bases:
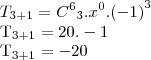

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
