(UFMG) Observe a figura
Nessa figura está representado o gráfico da função
f(x) = log2 1 / (ax + b).
Então, f (1) é igual a:
a) -3
b) -2
c) -1
d) -1/2
e) -1/3
resposta: letra b
Agradeço desde já.




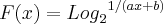 ? se for, ai da certo, faça o seguinte, ele te deu dois pontos, o ponto (0,0) e o ponto(5,-4). Basta substituí-los na função e encontrar os valores A e B.
? se for, ai da certo, faça o seguinte, ele te deu dois pontos, o ponto (0,0) e o ponto(5,-4). Basta substituí-los na função e encontrar os valores A e B.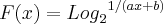 , a função equivalente será :
, a função equivalente será :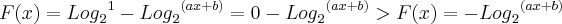
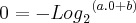 >
> 
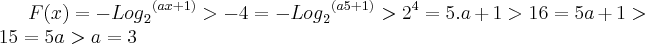
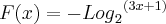





Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante