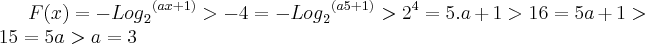por kamillanjb » Qua Mar 09, 2011 20:29
por kamillanjb » Qua Mar 09, 2011 20:29
(UFMG) Observe a figura
Nessa figura está representado o gráfico da função
f(x) = log2 1 / (ax + b).
Então, f (1) é igual a:
a) -3
b) -2
c) -1
d) -1/2
e) -1/3
resposta: letra b
Agradeço desde já.
- Anexos
-

- figura
- ajuda.jpg (5.45 KiB) Exibido 19663 vezes
-
kamillanjb
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Qua Fev 16, 2011 10:18
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Fabricio dalla » Qua Mar 09, 2011 22:04
por Fabricio dalla » Qua Mar 09, 2011 22:04
pow sei fazer n :(,se ele desse outro ponto pelo menos auhsuahusa
-
Fabricio dalla
- Colaborador Voluntário

-
- Mensagens: 111
- Registrado em: Sáb Fev 26, 2011 17:50
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Pedro123 » Qua Mar 09, 2011 22:54
por Pedro123 » Qua Mar 09, 2011 22:54
Camila, sua função deveria ser
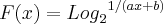
? se for, ai da certo, faça o seguinte, ele te deu dois pontos, o ponto (0,0) e o ponto(5,-4). Basta substituí-los na função e encontrar os valores A e B.
sendo a função a seguinte,
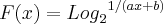
, a função equivalente será :
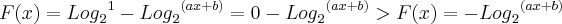
substituindo:
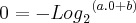
>

agora achando o A:
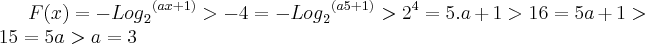
Logo a função é
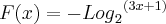

Ai está a resolução, tente usar o editor de formulas para evitar problemas desse tipo abraços.
qualquer duvida é so perguntar
-
Pedro123
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Qui Jun 10, 2010 22:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecanica - 1° Período
- Andamento: cursando
 por kamillanjb » Qua Mar 09, 2011 23:31
por kamillanjb » Qua Mar 09, 2011 23:31
A questão também foi passada para mim, da forma exposta. Eis a razão de não resolvê-la. Muito Obrigada
-
kamillanjb
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Qua Fev 16, 2011 10:18
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Pedro123 » Qua Mar 09, 2011 23:33
por Pedro123 » Qua Mar 09, 2011 23:33
ahhhm, sem problemas, pois é tambem dei uma pesquisada e achei algumas nessa formatação. abraços
-
Pedro123
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Qui Jun 10, 2010 22:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecanica - 1° Período
- Andamento: cursando
 por Raissa Dantas » Ter Jul 15, 2014 02:30
por Raissa Dantas » Ter Jul 15, 2014 02:30
Não entendi como fez pra achar o valor de A e B, pode dar mais detalhes, por favor?
-
Raissa Dantas
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Ter Jun 03, 2014 11:18
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Questão UFMG - função logarítmica
por Raissa Dantas » Ter Jul 15, 2014 02:34
- 0 Respostas
- 1116 Exibições
- Última mensagem por Raissa Dantas

Ter Jul 15, 2014 02:34
Funções
-
- (UFMG) Questão de Função
por Carolziiinhaaah » Sex Ago 13, 2010 17:34
- 1 Respostas
- 8050 Exibições
- Última mensagem por Douglasm

Sex Ago 13, 2010 18:02
Funções
-
- questao UFMG função
por WagnerSantos » Sáb Mar 12, 2011 15:16
- 3 Respostas
- 2117 Exibições
- Última mensagem por LuizAquino

Sáb Mar 12, 2011 19:56
Álgebra Elementar
-
- [Função Composta] Questão da UFMG, por favor.
por lucasf10 » Qui Out 02, 2014 17:27
- 1 Respostas
- 2149 Exibições
- Última mensagem por DanielFerreira

Sex Out 03, 2014 01:59
Funções
-
- [POLINÔMIOS] Questão da UFMG envolvendo divisão e função
por Romeo » Qua Nov 16, 2011 16:18
- 0 Respostas
- 1149 Exibições
- Última mensagem por Romeo

Qua Nov 16, 2011 16:18
Polinômios
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




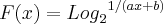 ? se for, ai da certo, faça o seguinte, ele te deu dois pontos, o ponto (0,0) e o ponto(5,-4). Basta substituí-los na função e encontrar os valores A e B.
? se for, ai da certo, faça o seguinte, ele te deu dois pontos, o ponto (0,0) e o ponto(5,-4). Basta substituí-los na função e encontrar os valores A e B.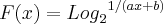 , a função equivalente será :
, a função equivalente será :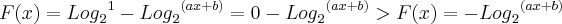
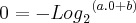 >
>