 por vanessitah » Sáb Mar 05, 2011 20:36
por vanessitah » Sáb Mar 05, 2011 20:36
1) (MACKENZI-SP) A raiz cubica de
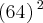
é:
Resolvi da seguinte maneira
![\sqrt[3]{{\left( 64) }^{2}} \right) \sqrt[3]{{\left( 64) }^{2}} \right)](/latexrender/pictures/791f0a8a4638a1e3cc63c6b20e798727.png)
=
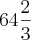
e nao soube continuar!
2)Tenho mais uma duvida de raiz, pois fiquei em duvida, do que resolver primeiro neste exemplo:
O valor de
![\left(\sqrt\sqrt[3]{2} \sqrt[]{2}\right){}^{8} \left(\sqrt\sqrt[3]{2} \sqrt[]{2}\right){}^{8}](/latexrender/pictures/d9c02dc865ce0f769edcd7048b58eafc.png)
é:
Resolvo o que ta dentro do parenteses 1°, ou elevo tudo que esta dentro a 8°?
Editado pela última vez por
vanessitah em Dom Mar 06, 2011 18:21, em um total de 2 vezes.
-
vanessitah
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Sáb Mar 05, 2011 18:07
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por MarceloFantini » Sáb Mar 05, 2011 20:52
por MarceloFantini » Sáb Mar 05, 2011 20:52
Vanessa, estou supondo que o que você quis dizer foi isso:
![\sqrt[3]{64^2} = 64^{\frac{2}{3}} \sqrt[3]{64^2} = 64^{\frac{2}{3}}](/latexrender/pictures/02e402bc589c731c0dc36c5fb71b43de.png)
.
Dica: procure escrever 64 como uma potência de 2, e depois trabalhe com propriedades de expoentes.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por vanessitah » Sáb Mar 05, 2011 21:59
por vanessitah » Sáb Mar 05, 2011 21:59
Nossa, é tao basico e eu fico inventando..rss
Ficou
![\sqrt[3]{{64}^{2}}=\sqrt[3]{{2}^{6}}={2}^{3}=8 \sqrt[3]{{64}^{2}}=\sqrt[3]{{2}^{6}}={2}^{3}=8](/latexrender/pictures/79447dba34ee155ef197756d08440834.png)
! Correto?
As diversas regras se misturam na minha cabeça, e as vezes fico perdida sem saber como e onde aplica-las.
Acredito que isto hora ou outra sera automaticamente mais facil!!
Vou treinando aqui...ate mais! Obrigada!
-
vanessitah
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Sáb Mar 05, 2011 18:07
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por LuizAquino » Dom Mar 06, 2011 09:08
por LuizAquino » Dom Mar 06, 2011 09:08
vanessitah escreveu:![\sqrt[3]{{64}^{2}}=\sqrt[3]{{2}^{6}}={2}^{3}=8 \sqrt[3]{{64}^{2}}=\sqrt[3]{{2}^{6}}={2}^{3}=8](/latexrender/pictures/79447dba34ee155ef197756d08440834.png)
Correto?
Não está correto. Lembre-se que

. Desse modo, quanto deve ser

?
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por JoaoGabriel » Dom Mar 06, 2011 10:06
por JoaoGabriel » Dom Mar 06, 2011 10:06
Resolução
\3/64²
\3/4096
16
-
JoaoGabriel
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Qua Ago 18, 2010 16:05
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Estudando para Engenharia Aeroespacial
- Andamento: cursando
 por vanessitah » Dom Mar 06, 2011 18:12
por vanessitah » Dom Mar 06, 2011 18:12
JoaoGabriel escreveu:Resolução
\3/64²
\3/4096
16
Ooops!!! Valeu!
-
vanessitah
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Sáb Mar 05, 2011 18:07
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por vanessitah » Dom Mar 06, 2011 18:13
por vanessitah » Dom Mar 06, 2011 18:13
LuizAquino escreveu:vanessitah escreveu:![\sqrt[3]{{64}^{2}}=\sqrt[3]{{2}^{6}}={2}^{3}=8 \sqrt[3]{{64}^{2}}=\sqrt[3]{{2}^{6}}={2}^{3}=8](/latexrender/pictures/79447dba34ee155ef197756d08440834.png)
Correto?
Não está correto. Lembre-se que

. Desse modo, quanto deve ser

?
Entendi meu erro! Esqueci do "quadrado"! Valeu a dica!
-
vanessitah
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Sáb Mar 05, 2011 18:07
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Abelardo » Seg Mar 07, 2011 01:00
por Abelardo » Seg Mar 07, 2011 01:00
Sim, deves começar por dentro do parenteses, facilitará bastante.
Lembre-se:
1º Da propriedade de multiplicação de potências;
2º Da equivalência entre potência e raiz, operações inversas;
3º Da propriedade da multiplicação de uma potência por outra, conserva a base e multiplica os expoentes.
Refresque sua mente com isso e poderás resolver sem dificuldade
Resposta:

.
-

Abelardo
- Colaborador Voluntário

-
- Mensagens: 159
- Registrado em: Qui Mar 03, 2011 01:45
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por vanessitah » Seg Mar 07, 2011 11:49
por vanessitah » Seg Mar 07, 2011 11:49
Abelardo escreveu:Sim, deves começar por dentro do parenteses, facilitará bastante.
Lembre-se:
1º Da propriedade de multiplicação de potências;
2º Da equivalência entre potência e raiz, operações inversas;
3º Da propriedade da multiplicação de uma potência por outra, conserva a base e multiplica os expoentes.
Refresque sua mente com isso e poderás resolver sem dificuldade
Resposta:

.
Este é um exercicio da UFRS, onde a resposta correta seria letra D...a raiz de 2 elevada ao cubo, multiplica a raiz de 2, onde todas estao dentro da primeira raiz, e elevadas a 8!
(UFRS) O valor de ( ![\left( \sqrt[]{\sqrt[3]{2\sqrt[]{2}}} \right){}^{8} \left( \sqrt[]{\sqrt[3]{2\sqrt[]{2}}} \right){}^{8}](/latexrender/pictures/fe7c04fbf99d2813f1c1e1fdbab37858.png) é:
é:A)
![2\sqrt[3]{{2}^{2}} 2\sqrt[3]{{2}^{2}}](/latexrender/pictures/14f4bba6a0b4a49cd8601a3f213682f0.png)
B)
![{2}^{6}\sqrt[3]{{2}^{2}} {2}^{6}\sqrt[3]{{2}^{2}}](/latexrender/pictures/21d8abed545415977d7fabea0ac31c0d.png)
C) 2
D) 4E) 8
-
vanessitah
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Sáb Mar 05, 2011 18:07
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por vanessitah » Seg Mar 07, 2011 12:04
por vanessitah » Seg Mar 07, 2011 12:04
vanessitah escreveu:Abelardo escreveu:Sim, deves começar por dentro do parenteses, facilitará bastante.
Lembre-se:
1º Da propriedade de multiplicação de potências;
2º Da equivalência entre potência e raiz, operações inversas;
3º Da propriedade da multiplicação de uma potência por outra, conserva a base e multiplica os expoentes.
Refresque sua mente com isso e poderás resolver sem dificuldade
Resposta:

.
Este é um exercicio da UFRS, onde a resposta correta seria letra D...a raiz de 2 elevada ao cubo, multiplica a raiz de 2, onde todas estao dentro da primeira raiz, e elevadas a 8!
(UFRS) O valor de ( ![\left( \sqrt[]{\sqrt[3]{2\sqrt[]{2}}} \right){}^{8} \left( \sqrt[]{\sqrt[3]{2\sqrt[]{2}}} \right){}^{8}](/latexrender/pictures/fe7c04fbf99d2813f1c1e1fdbab37858.png) é:
é:A)
![2\sqrt[3]{{2}^{2}} 2\sqrt[3]{{2}^{2}}](/latexrender/pictures/14f4bba6a0b4a49cd8601a3f213682f0.png)
B)
![{2}^{6}\sqrt[3]{{2}^{2}} {2}^{6}\sqrt[3]{{2}^{2}}](/latexrender/pictures/21d8abed545415977d7fabea0ac31c0d.png)
C) 2
D) 4E) 8
Estou seguindo este caminho:
![\sqrt[2]{\sqrt[24]{{2}^{8}}}\sqrt[2]{{2}^{8}} \sqrt[2]{\sqrt[24]{{2}^{8}}}\sqrt[2]{{2}^{8}}](/latexrender/pictures/3a7d08cb964aec45ed76917c45f7a12b.png)
=
![\sqrt[2]{\sqrt[48]{{2}^{64}}} \sqrt[2]{\sqrt[48]{{2}^{64}}}](/latexrender/pictures/e2ae6a73ab3a38ef890012aeea21701f.png)
=
Esta correto?
-
vanessitah
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Sáb Mar 05, 2011 18:07
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por vanessitah » Seg Mar 07, 2011 13:16
por vanessitah » Seg Mar 07, 2011 13:16
Imagine...todo mundo esta sujeito a erros de leitura!
Mas so uma dica! Nao entendi como foi a transformaçao do expoente em fraçao!?!
-
vanessitah
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Sáb Mar 05, 2011 18:07
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Abelardo » Seg Mar 07, 2011 13:48
por Abelardo » Seg Mar 07, 2011 13:48
É a operação inversa da radiciação. A operação inversa da adição é subtração, da multiplicação é a divisão e a da radiciação é a potenciação.
![\sqrt[2]{N}={N}^{\frac{1}{2}}
\sqrt[3]{N}={N}^{\frac{1}{3}}
\sqrt[4]{N}={N}^{\frac{1}{4}} \sqrt[2]{N}={N}^{\frac{1}{2}}
\sqrt[3]{N}={N}^{\frac{1}{3}}
\sqrt[4]{N}={N}^{\frac{1}{4}}](/latexrender/pictures/2c64000f341de89f68c56897c9ffa66c.png)
...
...
...
![\sqrt[a]{{x}^{b}}={x}^{\frac{b}{a}} \sqrt[a]{{x}^{b}}={x}^{\frac{b}{a}}](/latexrender/pictures/18a813b7e224d6a55490860a6753265f.png)
Vais eliminando as raízes de dentro para fora.
-

Abelardo
- Colaborador Voluntário

-
- Mensagens: 159
- Registrado em: Qui Mar 03, 2011 01:45
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [raízes de números complexos] Raízes de uma equação com grau
por karenfreitas » Seg Ago 22, 2016 19:08
- 1 Respostas
- 8111 Exibições
- Última mensagem por adauto martins

Sáb Ago 27, 2016 16:11
Números Complexos
-
- [Radiciação] Raízes dentro de raízes
por mottasky » Ter Set 13, 2011 22:00
- 2 Respostas
- 2567 Exibições
- Última mensagem por mottasky

Qui Set 15, 2011 15:52
Álgebra Elementar
-
- raízes.
por carolina camargo » Qua Jun 17, 2009 16:39
- 5 Respostas
- 2949 Exibições
- Última mensagem por Molina

Qua Jun 17, 2009 19:01
Funções
-
- Raízes
por aline2010 » Dom Ago 08, 2010 07:46
- 1 Respostas
- 1324 Exibições
- Última mensagem por MarceloFantini

Seg Ago 09, 2010 06:08
Sistemas de Equações
-
- raizes
por cristina » Qui Set 09, 2010 09:57
- 3 Respostas
- 1860 Exibições
- Última mensagem por MarceloFantini

Qui Set 09, 2010 17:52
Números Complexos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
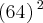 é:
é:![\sqrt[3]{{\left( 64) }^{2}} \right) \sqrt[3]{{\left( 64) }^{2}} \right)](/latexrender/pictures/791f0a8a4638a1e3cc63c6b20e798727.png) =
= 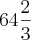 e nao soube continuar!
e nao soube continuar!![\left(\sqrt\sqrt[3]{2} \sqrt[]{2}\right){}^{8} \left(\sqrt\sqrt[3]{2} \sqrt[]{2}\right){}^{8}](/latexrender/pictures/d9c02dc865ce0f769edcd7048b58eafc.png) é:
é:
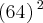 é:
é:![\sqrt[3]{{\left( 64) }^{2}} \right) \sqrt[3]{{\left( 64) }^{2}} \right)](/latexrender/pictures/791f0a8a4638a1e3cc63c6b20e798727.png) =
= 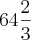 e nao soube continuar!
e nao soube continuar!![\left(\sqrt\sqrt[3]{2} \sqrt[]{2}\right){}^{8} \left(\sqrt\sqrt[3]{2} \sqrt[]{2}\right){}^{8}](/latexrender/pictures/d9c02dc865ce0f769edcd7048b58eafc.png) é:
é:
![\sqrt[3]{64^2} = 64^{\frac{2}{3}} \sqrt[3]{64^2} = 64^{\frac{2}{3}}](/latexrender/pictures/02e402bc589c731c0dc36c5fb71b43de.png) .
.

![\sqrt[3]{{64}^{2}}=\sqrt[3]{{2}^{6}}={2}^{3}=8 \sqrt[3]{{64}^{2}}=\sqrt[3]{{2}^{6}}={2}^{3}=8](/latexrender/pictures/79447dba34ee155ef197756d08440834.png) ! Correto?
! Correto?
 . Desse modo, quanto deve ser
. Desse modo, quanto deve ser  ?
?


. Desse modo, quanto deve ser
?

 .
.
.
![\left( \sqrt[]{\sqrt[3]{2\sqrt[]{2}}} \right){}^{8} \left( \sqrt[]{\sqrt[3]{2\sqrt[]{2}}} \right){}^{8}](/latexrender/pictures/fe7c04fbf99d2813f1c1e1fdbab37858.png) é:
é:![2\sqrt[3]{{2}^{2}} 2\sqrt[3]{{2}^{2}}](/latexrender/pictures/14f4bba6a0b4a49cd8601a3f213682f0.png)
![{2}^{6}\sqrt[3]{{2}^{2}} {2}^{6}\sqrt[3]{{2}^{2}}](/latexrender/pictures/21d8abed545415977d7fabea0ac31c0d.png)

.
é:
![\sqrt[2]{\sqrt[24]{{2}^{8}}}\sqrt[2]{{2}^{8}} \sqrt[2]{\sqrt[24]{{2}^{8}}}\sqrt[2]{{2}^{8}}](/latexrender/pictures/3a7d08cb964aec45ed76917c45f7a12b.png) =
= ![\sqrt[2]{\sqrt[48]{{2}^{64}}} \sqrt[2]{\sqrt[48]{{2}^{64}}}](/latexrender/pictures/e2ae6a73ab3a38ef890012aeea21701f.png) =
=
![{\left(\sqrt[]{\sqrt[3]{2\sqrt[]{2}}} \right)}^{8} {\left(\sqrt[]{\sqrt[3]{2\sqrt[]{2}}} \right)}^{8}](/latexrender/pictures/880072985221b291640616f24735030d.png)
![\Rightarrow {\left(\sqrt[]{\sqrt[3]{2.{2}^{\frac{1}{2}}}} \right)}^{8} \Rightarrow {\left(\sqrt[]{\sqrt[3]{2.{2}^{\frac{1}{2}}}} \right)}^{8}](/latexrender/pictures/3c9d7c577232fb477917a2a37dc96649.png)
![\Rightarrow {\left(\sqrt[]{\sqrt[3]{{2}^{\frac{3}{2}}}} \right)}^{8} \Rightarrow {\left(\sqrt[]{\sqrt[3]{{2}^{\frac{3}{2}}}} \right)}^{8}](/latexrender/pictures/72ec4726e8d2420689a9c3ccd93a4ee8.png)
![{\left(\sqrt[]{{2}^{\frac{1}{2}}} \right)}^{8} {\left(\sqrt[]{{2}^{\frac{1}{2}}} \right)}^{8}](/latexrender/pictures/bc090e52f27ec8771b646762b484bab5.png)
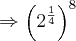


![{\left(\sqrt[]{\sqrt[3]{2\sqrt[]{2}}} \right)}^{8} {\left(\sqrt[]{\sqrt[3]{2\sqrt[]{2}}} \right)}^{8}](/latexrender/pictures/880072985221b291640616f24735030d.png)

![\sqrt[2]{N}={N}^{\frac{1}{2}}
\sqrt[3]{N}={N}^{\frac{1}{3}}
\sqrt[4]{N}={N}^{\frac{1}{4}} \sqrt[2]{N}={N}^{\frac{1}{2}}
\sqrt[3]{N}={N}^{\frac{1}{3}}
\sqrt[4]{N}={N}^{\frac{1}{4}}](/latexrender/pictures/2c64000f341de89f68c56897c9ffa66c.png)
![\sqrt[a]{{x}^{b}}={x}^{\frac{b}{a}} \sqrt[a]{{x}^{b}}={x}^{\frac{b}{a}}](/latexrender/pictures/18a813b7e224d6a55490860a6753265f.png)


 .
.



