 por kamillanjb » Qua Fev 16, 2011 19:47
por kamillanjb » Qua Fev 16, 2011 19:47
(UERJ)
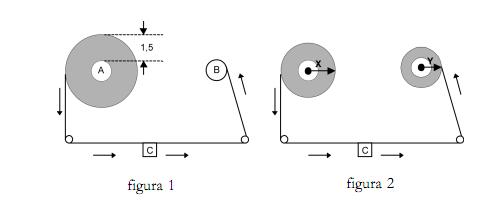
Observe a figura 1 que representa um leitor de áudio na posição de início de leitura.Os suportes
circulares A e B têm 1 cm de raio e uma fita de 90 m está totalmente enrolada em A formando uma
coroa circular de espessura 1,5 cm. A leitura da fita é feita pela peça C a uma velocidade constante.
À medida que a fita passa, nos suportes A e B, formam-se duas coroas circulares com raios maiores x
e y, respectivamente, como sugere a figura abaixo.
A . Esboce o gráfico que mostra o comprimento da fita enrolada em A, em função do tempo de leitura.
B. Calcule y em função de x.
(detalhe...eu n consigo ver os dados nessa questão, para mim esta faltando algo! Me ajudem, por favor!)
Resposta: b)
![\sqrt[2]{7,5-x²}, 1<=x<=2.5 \sqrt[2]{7,5-x²}, 1<=x<=2.5](/latexrender/pictures/d90249107c86fc7647cb3097ad123280.png)
- Anexos
-
- apagar.jpg (8.76 KiB) Exibido 6245 vezes
-
kamillanjb
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Qua Fev 16, 2011 10:18
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por gustavoluiss » Dom Fev 27, 2011 01:02
por gustavoluiss » Dom Fev 27, 2011 01:02
alguém dá uma luz nessa questão ai também
-
gustavoluiss
- Colaborador Voluntário

-
- Mensagens: 118
- Registrado em: Ter Nov 23, 2010 15:59
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por Fabricio dalla » Dom Fev 27, 2011 11:42
por Fabricio dalla » Dom Fev 27, 2011 11:42
agradeço se alguem resolve-la tbm muito boa!
-
Fabricio dalla
- Colaborador Voluntário

-
- Mensagens: 111
- Registrado em: Sáb Fev 26, 2011 17:50
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por LuizAquino » Dom Fev 27, 2011 17:25
por LuizAquino » Dom Fev 27, 2011 17:25
(A) Considere que a velocidade (constante) de leitura seja
c (dada em metros/segundo, por exemplo). Sendo assim, após
t segundos nós teremos
(90-ct) metros de fita enrolados no suporte A. Isto é, a função que fornece a quantidade de fita enrolada em A após
t segundos, será dada por
f(t)=90-ct. O gráfico para essa função está ilustrado abaixo.
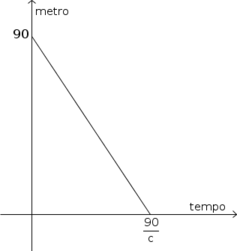
- grafico-tempo-metro.png (6.01 KiB) Exibido 6197 vezes
(B) A medida que o tempo passa, a coroa circular em A diminui a sua área. Já a coroa circular em B aumenta a sua área. A área que é perdida em A é acrescentada em B. Além disso, quando o suporte A está "cheio" temos que x=2,5, mas quando ele está "vazio" temos que x=1. Sendo assim, para
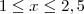
teremos a equação:
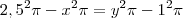
Desse equação, obtemos que

.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Fabricio dalla » Dom Fev 27, 2011 17:35
por Fabricio dalla » Dom Fev 27, 2011 17:35
obrigado luizaquino,aprendi muito msm com a resoluçao dessa questão
-
Fabricio dalla
- Colaborador Voluntário

-
- Mensagens: 111
- Registrado em: Sáb Fev 26, 2011 17:50
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Fabricio dalla » Dom Fev 27, 2011 17:54
por Fabricio dalla » Dom Fev 27, 2011 17:54
eu n tenho q incluir o raio de 1cm de y n ? aquele -1.pi q dizer q y ja vem com o raio de 1cm da polia ai subtrai?
-
Fabricio dalla
- Colaborador Voluntário

-
- Mensagens: 111
- Registrado em: Sáb Fev 26, 2011 17:50
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por LuizAquino » Dom Fev 27, 2011 18:43
por LuizAquino » Dom Fev 27, 2011 18:43
Fabricio dalla escreveu:eu n tenho q incluir o raio de 1cm de y n ? aquele -1.pi q dizer q y ja vem com o raio de 1cm da polia ai subtrai?
No início, o suporte B está "vazio" e portanto y=1. Com o passar do tempo, vai aparecendo a coroa circular de raio maior y e raio menor 1.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por kamillanjb » Dom Fev 27, 2011 20:10
por kamillanjb » Dom Fev 27, 2011 20:10
Pouxa, muito boa a resolução.
Já estava me levando a crer que não havia resposta ou modo de resolvê-la.
Muito Obrigada mesmo!!
-
kamillanjb
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Qua Fev 16, 2011 10:18
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Uerj 2001 - questão sobre conjuntos
por sspmat61 » Qui Mar 10, 2011 15:16
- 4 Respostas
- 14825 Exibições
- Última mensagem por Abelardo

Sex Mar 11, 2011 22:43
Álgebra Elementar
-
- (UERJ) - Questão de função linear
 por Levi23 » Qua Mar 11, 2009 22:28
por Levi23 » Qua Mar 11, 2009 22:28
- 1 Respostas
- 5309 Exibições
- Última mensagem por Levi23

Qua Mar 11, 2009 22:29
Funções
-
- Questão da Uerj função linear
por gustavoluiss » Seg Fev 07, 2011 22:24
- 12 Respostas
- 7776 Exibições
- Última mensagem por Santa Lucci

Ter Fev 08, 2011 01:24
Funções
-
- Questão UERJ
por phmarssal » Qua Nov 20, 2013 14:34
- 3 Respostas
- 2733 Exibições
- Última mensagem por Russman

Sáb Dez 07, 2013 00:25
Aritmética
-
- Questão UERJ
por phmarssal » Qua Nov 20, 2013 14:37
- 1 Respostas
- 1324 Exibições
- Última mensagem por Pessoa Estranha

Qui Nov 21, 2013 14:49
Aritmética
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sqrt[2]{7,5-x²}, 1<=x<=2.5 \sqrt[2]{7,5-x²}, 1<=x<=2.5](/latexrender/pictures/d90249107c86fc7647cb3097ad123280.png)



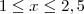 teremos a equação:
teremos a equação: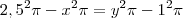
 .
.





