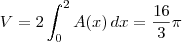por Isla » Qua Fev 23, 2011 12:12
por Isla » Qua Fev 23, 2011 12:12
Para calcular o volume de um solido cuja base é o disco

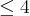
, tal que cada uma de suas seções transversias perpendiculares ao eixo 0x é um semicirculo.
Respondi assim:
volume desse sólido é dado por dV = A.dz, já que altura se expande no eixo Oz. A seção transversal do volume possui raio variável, tal que

, sendo p o raio.
Com a observação: "tal que cada uma de suas seções transversias perpendiculares ao eixo 0x é um semicirculo", tem se, um duplo cone (acima e abaixo da origem no eixo Oz), só que partido ao meio na linha do eixo Ox.
A área então do círculo partido será pi.p², (repetindo, p é o raio variável), então:
E agora me perdi...Socorro!
-
Isla
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qua Fev 23, 2011 00:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matematica
- Andamento: cursando
 por LuizAquino » Qua Fev 23, 2011 17:34
por LuizAquino » Qua Fev 23, 2011 17:34
Isla escreveu:Calcular o volume de um sólido cuja base é o disco

, tal que cada uma de suas seções transversais perpendiculares ao eixo Ox é um semicírculo.
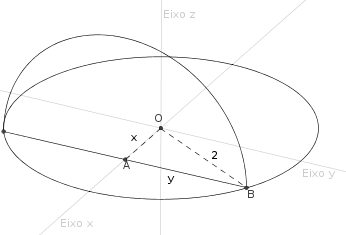
A figura acima ilustra o exercício.
- volume-semi-esfera.png (14.38 KiB) Exibido 3385 vezes
Como as seções transversais perpendiculares ao eixo Ox são semicírculos e a base é um círculo, então o sólido é uma semiesfera de raio 2. Sendo assim, já esperamos que o volume seja
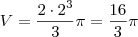
. Vamos confirmar isso aplicando integrais.
Cada semicírculo tem raio y. Notando que o triângulo OAB é retângulo, determinamos que a área de cada semicírculo será dada por

.
Sendo assim, o volume do sólido será dado por:
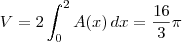
Editado pela última vez por
LuizAquino em Qua Fev 23, 2011 21:42, em um total de 2 vezes.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Elcioschin » Qua Fev 23, 2011 20:31
por Elcioschin » Qua Fev 23, 2011 20:31
Isla/Luis Aquino
É necessária uma pequena correção nos cálculos:
x² + y² =< 4 ------> R = 2 (e não R = 4) ----> y² = 4 - x²
dV = pi*y²dx -----> V = int[pi*(4 - x²)dx ----> Limite variando de x = 0 até x = 2
V = 4*pi*Int[dx] - pi*Int[x²dx]
V = 4*pi*x - pi*x³/3
Aplicando os limites ----> V = 4*pi*2 - pi*2³/3 ----> V = 8*pi - 8*pi/3 ----> V = 16*pi/3
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por LuizAquino » Qua Fev 23, 2011 21:40
por LuizAquino » Qua Fev 23, 2011 21:40
Elcioschin escreveu: É necessária uma pequena correção nos cálculos
Corrigido.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Aplicações do vetor gradiente] Aplicações das propriedades
 por TheoFerraz » Sex Out 28, 2011 16:14
por TheoFerraz » Sex Out 28, 2011 16:14
- 1 Respostas
- 3318 Exibições
- Última mensagem por LuizAquino

Sáb Out 29, 2011 11:16
Cálculo: Limites, Derivadas e Integrais
-
- [integrais] Calculando áreas - Integrais
 por Faby » Seg Set 19, 2011 10:55
por Faby » Seg Set 19, 2011 10:55
- 11 Respostas
- 8837 Exibições
- Última mensagem por LuizAquino

Qua Set 21, 2011 18:03
Cálculo: Limites, Derivadas e Integrais
-
- Aplicações da Derivada
por Bruhh » Qua Jun 02, 2010 19:00
- 2 Respostas
- 4783 Exibições
- Última mensagem por Bruhh

Sáb Jun 05, 2010 18:25
Cálculo: Limites, Derivadas e Integrais
-
- Aplicacoes de derivadas
 por aline_n » Qui Jun 02, 2011 17:29
por aline_n » Qui Jun 02, 2011 17:29
- 1 Respostas
- 3769 Exibições
- Última mensagem por LuizAquino

Qui Jun 02, 2011 20:34
Cálculo: Limites, Derivadas e Integrais
-
- [Derivadas - Aplicações]
por Scheu » Sex Mar 16, 2012 00:01
- 1 Respostas
- 1842 Exibições
- Última mensagem por MarceloFantini

Sex Mar 16, 2012 03:17
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

 , tal que cada uma de suas seções transversias perpendiculares ao eixo 0x é um semicirculo.
, tal que cada uma de suas seções transversias perpendiculares ao eixo 0x é um semicirculo. , sendo p o raio.
, sendo p o raio.

 , tal que cada uma de suas seções transversais perpendiculares ao eixo Ox é um semicírculo.
, tal que cada uma de suas seções transversais perpendiculares ao eixo Ox é um semicírculo.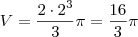 . Vamos confirmar isso aplicando integrais.
. Vamos confirmar isso aplicando integrais. .
.