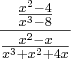
diga para quais valores de x é possível calcular essa expressão. Responda na forma de intervalos.
Simplifique a expressão de forma a obter uma expressão com um polinômio no numerador e um polinômio no denominador.
iguale a expressão dada à 2x e resolva a equação encontrada. para resolver essa equação você pode usar a expressão simplificada.
o primeiro item eu não consegui responder, pois a equação
 não possui solução em R.
não possui solução em R.o segundo item a minha resposta deu

e o terceiro item pedia para eu igualar o item anterior a 2x.
 =2x deu S={-1/2, 2}
=2x deu S={-1/2, 2}alguém poderia me ajudar nesta questão.



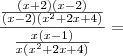






 . Portanto:
. Portanto:
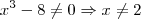
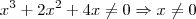 . Aqui, estamos considerando apenas as soluções reais.
. Aqui, estamos considerando apenas as soluções reais.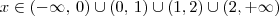
 . Se você primeiro simplificar para depois analisar, você teria que
. Se você primeiro simplificar para depois analisar, você teria que 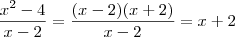 , e como não há restrições na expressão x+2 você diria que x pode ser qualquer número. Obviamente, isso está errado! O correto é que x pode ser qualquer número real exceto o 2. O erro aconteceu quando você simplificou o termo (x-2), o que
, e como não há restrições na expressão x+2 você diria que x pode ser qualquer número. Obviamente, isso está errado! O correto é que x pode ser qualquer número real exceto o 2. O erro aconteceu quando você simplificou o termo (x-2), o que 


 .
.
 :
: