 por Tayron » Ter Fev 15, 2011 09:45
por Tayron » Ter Fev 15, 2011 09:45
Bom estou com um dilema mais um amigo meu.
E bastante simples mais não nos recordamos, e o seguinte, se a gente pega um triângulo é quer saber quanto vale cada ângulo
é temos apenas a medida de 1 ângulo, no caso temos apenas a medida que o ângulo B vale 45º dai dividimos o triângulo em 2 partes,
vemos então que aparece um ângulo de 90º restando apenas +45º para a parte de cima do triângulo no lado A, fechamos assim 180º de um triângulo,
agora a duvida, podemos dizer que o outro triângulo como ele também tem 1 ângulo de 90º podemos dizer que o ângulo C vale 45º e o outro também 45º
neste exemplo exemplifiquei os outros dois ângulos como sendo "x" a duvida e está posso então dizer que ambos valem 45º como o do outro triângulo ?
Caso não como faço para calcular os outros ângulos ?
Abraços!

-
Tayron
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Qua Fev 09, 2011 15:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng.Cívil
- Andamento: cursando
 por Molina » Ter Fev 15, 2011 10:41
por Molina » Ter Fev 15, 2011 10:41
Bom dia, Tayron.
Foi um pouco difícil entender sua dúvida, mas vou tentar ser bem claro: Você não pode concluir que o outro ângulo seja 45 graus também. Isso só irá acontecer se tiver descrito que o triângulo é isósceles, pois daí teríamos dois ângulos iguais (por exemplo, os ângulos da base cada um com 45 graus) e o angulo superior com 90 graus, que quando dividido ao meio formaria 45 graus para cada lado. Neste exemplo dai sim podemos garantir que o outro ângulo é 45 graus.
Vou dar um exemplo de como poderia não ser 45 graus: Seja o triângulo ABC em que o ângulo B seja 45 graus (como no exemplo), o ângulo A seja 30 graus e o ângulo superior C seja 105 graus. Dividindo este triângulo eu teria dois novos triângulos sendo um deles com 45 graus do ângulo B, 90 graus devido ao perpendicularismo do lado AB e 45 restantes da divisão do ângulo C. Perceba que a outra parte do ângulo C não é 45 graus também, e sim 60 graus. Logo, o outro triângulo formado terá como graus: 30 do ângulo A + 90 do perpendicularismo do lado AB + 60 da divisão do ângulo C.
Ou seja, não posso concluir que o outro ângulo seja 45 graus também. Não há como definirmos qual este ângulo, a não ser se tivermos informação de algum outro ângulo ou então de dois lados deste triângulo, pois daí é possível usar a lei dos senos e/ou a lei dos cossenos e descobrir estes valores que te faltam.
Se ficou alguma dúvida informe. Gostaria de ter colocado algumas imagens, mas para agora não está sendo possível.
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Tayron » Ter Fev 15, 2011 10:48
por Tayron » Ter Fev 15, 2011 10:48
Ajudou sim bastante, tirou nossa duvida.
Mais agora que entendi não estamos conseguindo calcular a altura do mesmo o exercício e aquela mesma imagem só que com algumas medidas.

Duvida saber a Altura do triangulo, é quanto valem os outros lados
-
Tayron
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Qua Fev 09, 2011 15:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng.Cívil
- Andamento: cursando
 por Molina » Ter Fev 15, 2011 11:02
por Molina » Ter Fev 15, 2011 11:02
Vamos chamar esta altura de h, como é normalmente chamada.
Pela definição de seno sabemos que:

Podemos usar esta informação no triângulo da esquerda <---, pois temos o ângulo, a hipotenusa e queremos descobrir h que faz o papel de cateto oposto ao ângulo de 45 graus. Então:


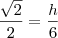
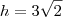
Era isso que você queria descobrir?
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Tayron » Ter Fev 15, 2011 11:45
por Tayron » Ter Fev 15, 2011 11:45
Isso mesmo cheguei na mesma altura só que os ângulos do triângulo da direita não tem como eu descobrir a partir da altura ou com esses dados tem ?
-
Tayron
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Qua Fev 09, 2011 15:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng.Cívil
- Andamento: cursando
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [ajuda urgente] dúvida básica
por ricardosanto » Qui Mai 03, 2012 08:19
- 1 Respostas
- 1807 Exibições
- Última mensagem por Russman

Qui Mai 03, 2012 11:03
Cálculo: Limites, Derivadas e Integrais
-
- Equação - Dúvida básica sobre a proporcionalidade de equação
por FelipeGM » Qui Jan 12, 2012 19:05
- 4 Respostas
- 7721 Exibições
- Última mensagem por FelipeGM

Sáb Jan 14, 2012 13:16
Álgebra Elementar
-
- Exercício sobre triângulos
 por LuizCarlos » Sáb Mar 31, 2012 17:12
por LuizCarlos » Sáb Mar 31, 2012 17:12
- 7 Respostas
- 7498 Exibições
- Última mensagem por LuizCarlos

Sáb Mar 31, 2012 18:53
Trigonometria
-
- Duvida sobre ajuda matemática
por zenildo » Sáb Set 07, 2013 19:28
- 1 Respostas
- 957 Exibições
- Última mensagem por temujin

Sáb Set 07, 2013 21:52
Álgebra Elementar
-
- [derivadas]Ajuda básica
por MarlonMO250 » Dom Fev 24, 2013 16:37
- 3 Respostas
- 2162 Exibições
- Última mensagem por Russman

Dom Fev 24, 2013 20:21
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.







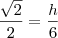
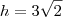
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
