E bastante simples mais não nos recordamos, e o seguinte, se a gente pega um triângulo é quer saber quanto vale cada ângulo
é temos apenas a medida de 1 ângulo, no caso temos apenas a medida que o ângulo B vale 45º dai dividimos o triângulo em 2 partes,
vemos então que aparece um ângulo de 90º restando apenas +45º para a parte de cima do triângulo no lado A, fechamos assim 180º de um triângulo,
agora a duvida, podemos dizer que o outro triângulo como ele também tem 1 ângulo de 90º podemos dizer que o ângulo C vale 45º e o outro também 45º
neste exemplo exemplifiquei os outros dois ângulos como sendo "x" a duvida e está posso então dizer que ambos valem 45º como o do outro triângulo ?
Caso não como faço para calcular os outros ângulos ?
Abraços!







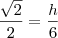
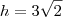
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.