 por Raphael Feitas10 » Qui Jan 13, 2011 13:18
por Raphael Feitas10 » Qui Jan 13, 2011 13:18
Brother tou com duvida nessa aqui...
Achar os numeros que devem ser adicionados aos termos da fração 5/13 para que se obtenha uma fração que seja o dobro dela e na qual a soma dos termos seja 46? a resposta é 15 e 13
brother conseguie montar ate aqui só...
\frac{5+x}{13+y}=1\Rightarrow x+y=46
-
Raphael Feitas10
- Colaborador Voluntário

-
- Mensagens: 162
- Registrado em: Ter Jan 04, 2011 20:10
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por VtinxD » Qui Jan 13, 2011 14:52
por VtinxD » Qui Jan 13, 2011 14:52
Acho que faltou só uma coisa....

, o raciocínio esta no post acima.
-
VtinxD
- Usuário Parceiro

-
- Mensagens: 64
- Registrado em: Dom Ago 15, 2010 18:29
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Bacharelado em Matematica
- Andamento: cursando
 por Raphael Feitas10 » Qui Jan 13, 2011 20:13
por Raphael Feitas10 » Qui Jan 13, 2011 20:13
Fantini escreveu: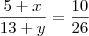
e

Fratine como faz pra achar o 15 e 13 fiz aqui mas ñ conseguei ñ brother?
-
Raphael Feitas10
- Colaborador Voluntário

-
- Mensagens: 162
- Registrado em: Ter Jan 04, 2011 20:10
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por MarceloFantini » Qui Jan 13, 2011 20:29
por MarceloFantini » Qui Jan 13, 2011 20:29
Obrigado Vtin, passou despercebido. E Raphael, é só você resolver o sistema de duas equações e duas incógnitas.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Raphael Feitas10 » Sex Jan 14, 2011 01:28
por Raphael Feitas10 » Sex Jan 14, 2011 01:28
Brother essa aqui tbm é um pouco chata saca só...
Um numero é tal que a soma de seus dois algarismo é 7.Calcule este numero sabendo que,invertendo seus algarismos,o numero resultante vale duas vezes o primeiro,mais duas unidades. R: 25
Cheguei ate aqui e travei...

-
Raphael Feitas10
- Colaborador Voluntário

-
- Mensagens: 162
- Registrado em: Ter Jan 04, 2011 20:10
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por Raphael Feitas10 » Sex Jan 14, 2011 23:10
por Raphael Feitas10 » Sex Jan 14, 2011 23:10
Raphael Feitas10 escreveu:Brother essa aqui tbm é um pouco chata saca só...
Um numero é tal que a soma de seus dois algarismo é 7.Calcule este numero sabendo que,invertendo seus algarismos,o numero resultante vale duas vezes o primeiro,mais duas unidades. R: 25
Cheguei ate aqui e travei...

Alguem me ajuda nessa questão aqui por favor...
-
Raphael Feitas10
- Colaborador Voluntário

-
- Mensagens: 162
- Registrado em: Ter Jan 04, 2011 20:10
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por Elcioschin » Sáb Jan 15, 2011 13:49
por Elcioschin » Sáb Jan 15, 2011 13:49
Raphael
Cada tópico deve conter apenas uma questão.
Mesmo assim vou dar a dica: tire o valor de y na 1ª equação e substitua na 2ª e vc obterá uma equação do 2º grau em x
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por Dan » Seg Jan 17, 2011 12:48
por Dan » Seg Jan 17, 2011 12:48
Eu acho que aí tem um erro de interpretação.
O dobro de
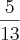
é
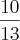
.
-

Dan
- Colaborador Voluntário

-
- Mensagens: 101
- Registrado em: Seg Set 14, 2009 09:44
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Raphael Feitas10 » Seg Jan 17, 2011 15:31
por Raphael Feitas10 » Seg Jan 17, 2011 15:31
Dan escreveu:Eu acho que aí tem um erro de interpretação.
O dobro de
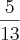
é
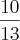
.
Brother fiz aqui desse jeito q vc interpretou mas tbm deu errado nem achei 15 e nem 13,que questão xata essa ver se vc consegue responder ela aew.
-
Raphael Feitas10
- Colaborador Voluntário

-
- Mensagens: 162
- Registrado em: Ter Jan 04, 2011 20:10
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por Dan » Seg Jan 17, 2011 19:56
por Dan » Seg Jan 17, 2011 19:56
O que acontece é que é a soma dos termos da segunda fração que deve dar 46. Assim,

.
Ou seja, na verdade

, pois não é a soma de x e y que dá 46, mas a soma dos termos da segunda fração. Veja pelo enunciado: "uma fração que seja o dobro dela e
na qual a soma dos termos seja 46".
Dá certo assim:

Tente de novo.
-

Dan
- Colaborador Voluntário

-
- Mensagens: 101
- Registrado em: Seg Set 14, 2009 09:44
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Renato_RJ » Ter Jan 18, 2011 19:11
por Renato_RJ » Ter Jan 18, 2011 19:11
O Dan matou a charada, fazendo

teremos:
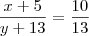
Relembrando algumas propriedades básicas de proporções:
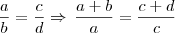
Aplicando a propriedade, teremos:

Como

teremos:

Bem, o

sai facilmente....
Abraços,
Renato.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
 por Raphael Feitas10 » Qua Jan 19, 2011 00:06
por Raphael Feitas10 » Qua Jan 19, 2011 00:06
Brother muito obrg valeu mesmo abraço.
-
Raphael Feitas10
- Colaborador Voluntário

-
- Mensagens: 162
- Registrado em: Ter Jan 04, 2011 20:10
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por Renato_RJ » Qua Jan 19, 2011 00:20
por Renato_RJ » Qua Jan 19, 2011 00:20
Raphael Feitas10 escreveu:Brother muito obrg valeu mesmo abraço.
Cara, eu sumi por uns dias do forum e achava que esse problema já tinha sido resolvido... Aí entrei hoje e vi o post do Dan, ele matou toda a charada, aí ficou fácil resolver...
Fico feliz que tenha lhe ajudado, qualquer coisa posta aí...
[ ] 's
Renato.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
 por Raphael Feitas10 » Qua Jan 19, 2011 00:40
por Raphael Feitas10 » Qua Jan 19, 2011 00:40
Renato_RJ escreveu:Raphael Feitas10 escreveu:Brother muito obrg valeu mesmo abraço.
Cara, eu sumi por uns dias do forum e achava que esse problema já tinha sido resolvido... Aí entrei hoje e vi o post do Dan, ele matou toda a charada, aí ficou fácil resolver...
Fico feliz que tenha lhe ajudado, qualquer coisa posta aí...
[ ] 's
Renato.
Postei duas questões agorinha aew brother que ñ resolvie saca elas aew falow abraço.
-
Raphael Feitas10
- Colaborador Voluntário

-
- Mensagens: 162
- Registrado em: Ter Jan 04, 2011 20:10
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Números Complexos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- números inteiros
por thadeu » Qui Nov 19, 2009 11:41
- 2 Respostas
- 2071 Exibições
- Última mensagem por thadeu

Qui Nov 19, 2009 13:46
Álgebra Elementar
-
- numeros inteiros
por edwilsoncrep » Qui Mar 04, 2010 20:03
- 5 Respostas
- 6391 Exibições
- Última mensagem por adriana_borges

Dom Mai 09, 2010 12:04
Sequências
-
- Numeros inteiros
por Raphael Feitas10 » Qua Jan 05, 2011 00:16
- 3 Respostas
- 2685 Exibições
- Última mensagem por PedroSantos

Qua Jan 05, 2011 19:49
Cálculo: Limites, Derivadas e Integrais
-
- Numeros inteiros 2
por Raphael Feitas10 » Qua Jan 19, 2011 00:28
- 1 Respostas
- 2893 Exibições
- Última mensagem por Renato_RJ

Qua Jan 19, 2011 01:52
Funções
-
- Numeros inteiros 3
por Raphael Feitas10 » Qua Jan 19, 2011 17:03
- 1 Respostas
- 1661 Exibições
- Última mensagem por Molina

Qua Jan 19, 2011 21:49
Conversão de Unidades
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




 , o raciocínio esta no post acima.
, o raciocínio esta no post acima.
e







e
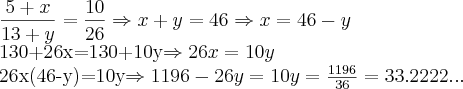

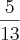 é
é 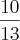 .
.
é
.

 .
. , pois não é a soma de x e y que dá 46, mas a soma dos termos da segunda fração. Veja pelo enunciado: "uma fração que seja o dobro dela e na qual a soma dos termos seja 46".
, pois não é a soma de x e y que dá 46, mas a soma dos termos da segunda fração. Veja pelo enunciado: "uma fração que seja o dobro dela e na qual a soma dos termos seja 46".

 teremos:
teremos: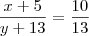
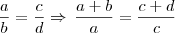

 teremos:
teremos:
 sai facilmente....
sai facilmente....








