 por lizbortolli » Sáb Nov 20, 2010 00:07
por lizbortolli » Sáb Nov 20, 2010 00:07
1- calcule o valor de x usando em cada caso as propriedades operatórias:
a)

b)
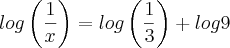
2-adimitindo que log2

0,3 , qual é o valor de:
![log\left(\frac{20}{\sqrt[5]{4}} \right) log\left(\frac{20}{\sqrt[5]{4}} \right)](/latexrender/pictures/c489fe56d6ecdb7cf7b68b7b9ea43428.png)
-
lizbortolli
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sex Nov 19, 2010 23:44
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: agronomia
- Andamento: cursando
 por Loretto » Sáb Nov 20, 2010 02:34
por Loretto » Sáb Nov 20, 2010 02:34
2.log x = log 3 + log 4
2.log x = log (3.4)
2.log x = log 12
2.log x = log 2^2.3
2.log x = 2.log 2.3
2.log x = 2.log 6
log x = log 6
10^log6 = x
x = 6
-------------------------
a^log b (na base a) = b
-
Loretto
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Dom Jul 25, 2010 01:35
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: exatas
- Andamento: cursando
 por 0 kelvin » Sáb Nov 20, 2010 12:41
por 0 kelvin » Sáb Nov 20, 2010 12:41
Estranhei essa passagem log 12 = 2 log (2 x 3)
Pq log (2 log 6) é (log 36).
Edit: ah sim,

.

o negativo é descartado pela definição do log.
Pois
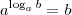
b) Lembre que

2- Lembre que
![\sqrt[5]{4} = 4^{\frac{1}{5}} \sqrt[5]{4} = 4^{\frac{1}{5}}](/latexrender/pictures/8077175832c205e140f8234588c7f3ee.png)
Log 20. 20 não dá pra fatorar numa base só, vai ficar 2 x 2 x 5. Mas 5 pode ser escrito como 10/2, aí é só usar a propriedade do quociente, pois log de 10 na base 10 é 1 e log de 2 esta dado como 0,3 aprox.
Editado pela última vez por
0 kelvin em Sáb Nov 20, 2010 14:08, em um total de 1 vez.
-
0 kelvin
- Usuário Parceiro

-
- Mensagens: 78
- Registrado em: Dom Out 31, 2010 16:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciencias atmosfericas
- Andamento: cursando
 por Lorettto » Seg Dez 20, 2010 14:59
por Lorettto » Seg Dez 20, 2010 14:59
Questão 2:
log (20 / raiz quinta (4)) = log ( 20 / (4 ^(1/5)) = log (20 / (2²) ^ (1/5)) = log (20 / (2 ^ (2/5))
Racionalizando (tirando a raiz do denominador), multiplicamos em cima e em baixo por 2 ^ (3/5)
= log (20 * (2 ^(3/5)) / (2 ^ (2/5) * 2 ^ (3/5)) = log ( 20 * (2 ^ (3/5)) / 2) = log (10 * (2 ^ (3/5))
= log 10 + log (2 ^(3/5)) = 1 + 3/5 * log 2 = 1 + 0,6 * log 2
Considerando log 2 = 0,3 obtemos o valor aproximado
= 1 + 0,6 * 0,3 = 1 + 0,18 = 1,18
"RESPOSTA DE PAULISTA."
Abraço,
Loreto
-
Lorettto
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Sáb Nov 27, 2010 01:17
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- ajuda com logaritimos
por Andersonborges » Sáb Fev 26, 2011 16:57
- 7 Respostas
- 3780 Exibições
- Última mensagem por Molina

Qui Mar 03, 2011 00:18
Logaritmos
-
- continuando com logaritimos
por Andersonborges » Sáb Fev 26, 2011 17:10
- 1 Respostas
- 1435 Exibições
- Última mensagem por Molina

Sáb Fev 26, 2011 18:27
Logaritmos
-
- Equação de logarítimos
por lilianers » Sex Mar 29, 2013 21:27
- 1 Respostas
- 1576 Exibições
- Última mensagem por young_jedi

Sáb Mar 30, 2013 11:54
Logaritmos
-
- Equação de logarítimos
por lilianers » Sex Mar 29, 2013 21:29
- 2 Respostas
- 2106 Exibições
- Última mensagem por lilianers

Sex Mar 29, 2013 22:08
Logaritmos
-
- LIMITES de exponenciais e logaritimos
por inkz » Qua Dez 05, 2012 16:13
- 1 Respostas
- 1691 Exibições
- Última mensagem por e8group

Qua Dez 05, 2012 20:45
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

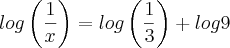
 0,3 , qual é o valor de:
0,3 , qual é o valor de:![log\left(\frac{20}{\sqrt[5]{4}} \right) log\left(\frac{20}{\sqrt[5]{4}} \right)](/latexrender/pictures/c489fe56d6ecdb7cf7b68b7b9ea43428.png)


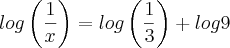
 0,3 , qual é o valor de:
0,3 , qual é o valor de:![log\left(\frac{20}{\sqrt[5]{4}} \right) log\left(\frac{20}{\sqrt[5]{4}} \right)](/latexrender/pictures/c489fe56d6ecdb7cf7b68b7b9ea43428.png)


 .
.  o negativo é descartado pela definição do log.
o negativo é descartado pela definição do log.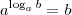

![\sqrt[5]{4} = 4^{\frac{1}{5}} \sqrt[5]{4} = 4^{\frac{1}{5}}](/latexrender/pictures/8077175832c205e140f8234588c7f3ee.png)



