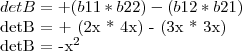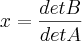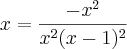por natanskt » Sáb Nov 20, 2010 10:46
por natanskt » Sáb Nov 20, 2010 10:46
considere as matrizes
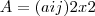
e

definidas por
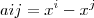
e
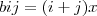
,xeR* . se a função de
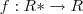
é definida por

,então para
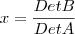
o valor de f(x) é:
a-)

b-)

c-)

d-)

minha tentativa de resolução:
os elementos de a e b coloquei assim a11 a12 a13 etc,(vcs entenderam)
depois eu apliquei a definição nos dois:

e
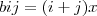
esse X eu chutei valor pra ele
depois de calcular a definição eu calculei o det
e dividi um pelo outro o valor eu coloquei aqui f(x)=1/x
o resultado não bate eu acho que fiz tudo errado
valeu!
-
natanskt
- Colaborador Voluntário

-
- Mensagens: 176
- Registrado em: Qua Out 06, 2010 14:56
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: nenhum
- Andamento: cursando
 por MarceloFantini » Sáb Nov 20, 2010 12:27
por MarceloFantini » Sáb Nov 20, 2010 12:27
Você não deve chutar valores para o x. Monte as matrizes e depois calcule os determinantes e faça a razão. Em seguida, jogue na função.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por natanskt » Seg Nov 22, 2010 14:44
por natanskt » Seg Nov 22, 2010 14:44
alguem aew me ajuda.que eu não to conmseguindo.
acho que to no caminho certo,mais faz hora que eu tento e não dá certo.
-
natanskt
- Colaborador Voluntário

-
- Mensagens: 176
- Registrado em: Qua Out 06, 2010 14:56
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: nenhum
- Andamento: cursando
 por monicadiasf » Sex Abr 20, 2012 16:00
por monicadiasf » Sex Abr 20, 2012 16:00
Não sei usar o Latex direito -.-
Mas vou ajudar!
Encontrando os elementos da matriz A e o seu respectivo determinante:

![detA = + (a11 * a22) - (a12 * a21)
detA = 0 - [(x^2 -x)(x - x^2)]
detA = x^2(x-1)^2 detA = + (a11 * a22) - (a12 * a21)
detA = 0 - [(x^2 -x)(x - x^2)]
detA = x^2(x-1)^2](/latexrender/pictures/89c6e7217928794ca614d6c1709b39c1.png)
Encontrando os elementos da matriz B e o seu respectivo determinante:

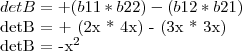
Sendo que:
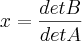
Então:
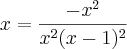

Substituíndo esse valor de x na função dada:


Logo, a resposta é a letra

-
monicadiasf
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sex Abr 20, 2012 15:01
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Fisioterapia
- Andamento: cursando
Voltar para Matrizes e Determinantes
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Determinante
por Jessi » Seg Abr 20, 2009 16:10
- 1 Respostas
- 3184 Exibições
- Última mensagem por Molina

Seg Abr 20, 2009 17:04
Matrizes e Determinantes
-
- Determinante
por DanielRJ » Sex Set 10, 2010 22:00
- 5 Respostas
- 5390 Exibições
- Última mensagem por MarceloFantini

Dom Set 12, 2010 17:18
Matrizes e Determinantes
-
- Determinante
por DanielRJ » Sáb Set 11, 2010 18:47
- 4 Respostas
- 4679 Exibições
- Última mensagem por DanielRJ

Dom Set 12, 2010 12:56
Matrizes e Determinantes
-
- Determinante
por DanielRJ » Dom Set 12, 2010 15:54
- 3 Respostas
- 3970 Exibições
- Última mensagem por MarceloFantini

Seg Set 13, 2010 00:03
Matrizes e Determinantes
-
- (ITA) DETERMINANTE
por natanskt » Sáb Nov 20, 2010 10:26
- 4 Respostas
- 4297 Exibições
- Última mensagem por vitall

Ter Jan 04, 2011 02:42
Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
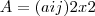 e
e  definidas por
definidas por 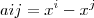 e
e 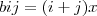 ,xeR* . se a função de
,xeR* . se a função de 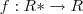 é definida por
é definida por  ,então para
,então para 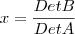 o valor de f(x) é:
o valor de f(x) é:



 e
e 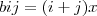 esse X eu chutei valor pra ele
esse X eu chutei valor pra ele




![detA = + (a11 * a22) - (a12 * a21)
detA = 0 - [(x^2 -x)(x - x^2)]
detA = x^2(x-1)^2 detA = + (a11 * a22) - (a12 * a21)
detA = 0 - [(x^2 -x)(x - x^2)]
detA = x^2(x-1)^2](/latexrender/pictures/89c6e7217928794ca614d6c1709b39c1.png)