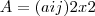 e
e  definidas por
definidas por 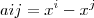 e
e 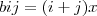 ,xeR* . se a função de
,xeR* . se a função de 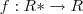 é definida por
é definida por  ,então para
,então para 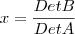 o valor de f(x) é:
o valor de f(x) é:a-)

b-)

c-)

d-)

minha tentativa de resolução:
os elementos de a e b coloquei assim a11 a12 a13 etc,(vcs entenderam)
depois eu apliquei a definição nos dois:
 e
e 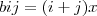 esse X eu chutei valor pra ele
esse X eu chutei valor pra eledepois de calcular a definição eu calculei o det
e dividi um pelo outro o valor eu coloquei aqui f(x)=1/x
o resultado não bate eu acho que fiz tudo errado
valeu!





![detA = + (a11 * a22) - (a12 * a21)
detA = 0 - [(x^2 -x)(x - x^2)]
detA = x^2(x-1)^2 detA = + (a11 * a22) - (a12 * a21)
detA = 0 - [(x^2 -x)(x - x^2)]
detA = x^2(x-1)^2](/latexrender/pictures/89c6e7217928794ca614d6c1709b39c1.png)

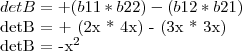
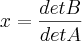
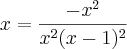






 .
.
 :
: