 por weverton » Seg Nov 08, 2010 16:11
por weverton » Seg Nov 08, 2010 16:11
1- dados A=logx, B=log(x+2) e C=log3, calcule x para que se tenha A+B=C
me ajudem por favor,desde ja agradeço!
-
weverton
- Usuário Parceiro

-
- Mensagens: 62
- Registrado em: Sex Mai 14, 2010 01:27
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: enfermagem
- Andamento: formado
 por MarceloFantini » Seg Nov 08, 2010 16:52
por MarceloFantini » Seg Nov 08, 2010 16:52
Substituia A, B e C e use propriedades.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por weverton » Seg Nov 08, 2010 17:28
por weverton » Seg Nov 08, 2010 17:28
ola sera q vc nao poderia me dar um exemplo e q eu nao entendo muito de log !
-
weverton
- Usuário Parceiro

-
- Mensagens: 62
- Registrado em: Sex Mai 14, 2010 01:27
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: enfermagem
- Andamento: formado
 por MarceloFantini » Seg Nov 08, 2010 17:37
por MarceloFantini » Seg Nov 08, 2010 17:37
Você conhece as propriedades?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por weverton » Qua Nov 10, 2010 01:14
por weverton » Qua Nov 10, 2010 01:14
e a multiplicação,divisão e exponenciação !
axo q e isso estou certo?
-
weverton
- Usuário Parceiro

-
- Mensagens: 62
- Registrado em: Sex Mai 14, 2010 01:27
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: enfermagem
- Andamento: formado
 por weverton » Qua Nov 10, 2010 01:35
por weverton » Qua Nov 10, 2010 01:35
so pra eu entender a soma de log x + log(x+2) =C e isso?
-
weverton
- Usuário Parceiro

-
- Mensagens: 62
- Registrado em: Sex Mai 14, 2010 01:27
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: enfermagem
- Andamento: formado
 por MarceloFantini » Qua Nov 10, 2010 01:43
por MarceloFantini » Qua Nov 10, 2010 01:43
Sim, e lembre-se que
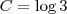
, portanto aplique a propriedade da soma de logaritmos, encontre possíveis valores de x e verifique condições de existência. Após isso, terá as respostas.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Me ajudem
por geriane » Qui Abr 22, 2010 16:01
- 1 Respostas
- 2830 Exibições
- Última mensagem por Molina

Qui Abr 22, 2010 20:48
Desafios Fáceis
-
- me ajudem ai !!
por weverton » Ter Jun 15, 2010 23:45
- 1 Respostas
- 1634 Exibições
- Última mensagem por Mathmatematica

Qua Jun 16, 2010 01:18
Sistemas de Equações
-
- me ajudem ai!!!
 por weverton » Qui Jul 08, 2010 17:15
por weverton » Qui Jul 08, 2010 17:15
- 2 Respostas
- 8406 Exibições
- Última mensagem por Lucio Carvalho

Qui Jul 08, 2010 19:50
Estatística
-
- me ajudem
por weverton » Qui Out 07, 2010 17:34
- 1 Respostas
- 1660 Exibições
- Última mensagem por MarceloFantini

Qui Out 07, 2010 18:07
Geometria Analítica
-
- Me ajudem!
por paulag » Qua Nov 10, 2010 21:30
- 1 Respostas
- 1431 Exibições
- Última mensagem por paulag

Qua Nov 10, 2010 23:12
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.










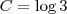 , portanto aplique a propriedade da soma de logaritmos, encontre possíveis valores de x e verifique condições de existência. Após isso, terá as respostas.
, portanto aplique a propriedade da soma de logaritmos, encontre possíveis valores de x e verifique condições de existência. Após isso, terá as respostas.

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.