Estou sentindo dificuldade em resolver alguns exercícios de trigonometria e gostaria muitíssimo que me ajudassem.

Sabendo que cos(x) = 1/3 e que 3pi/2 < x <2pi, calcule:
a) sen(x + pi/6)
Eu acho que devo estar cometendo erros de matemática básica pois nunca consigo chegar à solução final!
Sei que ao mostrar 3pi/2 < x < 2pi (a mesma coisa que 270°< x < 360°) o exercício me diz que x encontra-se no 4 quadrante. Depois, tenho que utilizar a fórmula sen(a+b)= sen a.cos b + sen b.cos a para
chegar à solução. Acredito que durante a resolução do exercício também terei que me vale da fórmula sen x² + cos x² = 1, já que foi me dado apenas o valor do cos(x) e não do sen(x).
Ficaria muito grato se alguém puder me dar uma explicação detalhada de como resolver o problema.
Agradeço desde já!
Obs.: Infelizmente senti dificuldade para escrever o problema em LaTeX. Espero que compreendam.


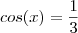 e
e 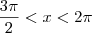 , então
, então 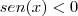





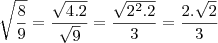
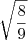 em resp dissertativa estaria certo tb a unica coisa eh que
em resp dissertativa estaria certo tb a unica coisa eh que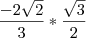 :
: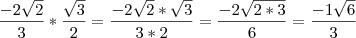

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)