 por LBT » Dom Out 31, 2010 23:49
por LBT » Dom Out 31, 2010 23:49
Boas, estou a estudar para um exame e surgiiu me este problema
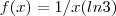
com

Como calculo este integral? Tenho de fazer por partes certo?
O que eu pensei foi em
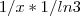

e

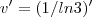
e

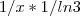 -
- 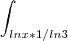
dx, mas como até aqui ja deve estar tudo mal, pois eu não percebi muito bem esta regra, se algue, puder explicar, ficaria muito grato!
Já agora como fazem a primitiva de

?
Onde posso encontrar um bom artigo sobre derivação por partes?
Obrigado
Editado pela última vez por
LBT em Seg Nov 01, 2010 12:18, em um total de 1 vez.
-
LBT
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Seg Out 18, 2010 16:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Informatica
- Andamento: cursando
 por Anniinha » Seg Nov 01, 2010 00:59
por Anniinha » Seg Nov 01, 2010 00:59
Escreva sua questão com as fórmulas da LaTeX e quem sabe poderei te ajudar.
-

Anniinha
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Dom Out 31, 2010 01:23
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Geofísica
- Andamento: cursando
 por Anniinha » Seg Nov 01, 2010 01:01
por Anniinha » Seg Nov 01, 2010 01:01
Escreva sua questão com as fórmulas da LaTeX e quem sabe poderei te ajudar.
-

Anniinha
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Dom Out 31, 2010 01:23
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Geofísica
- Andamento: cursando
 por LBT » Seg Nov 01, 2010 12:20
por LBT » Seg Nov 01, 2010 12:20
Anniinha escreveu:Escreva sua questão com as fórmulas da LaTeX e quem sabe poderei te ajudar.
Desculpa! Acho que ja consegui meter isso mais ao menos!
Obrigado pela atenção
-
LBT
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Seg Out 18, 2010 16:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Informatica
- Andamento: cursando
 por Neperiano » Seg Nov 01, 2010 13:04
por Neperiano » Seg Nov 01, 2010 13:04
Ola
Tome u como 1/ln3, pois voce só sabe derivar isso du= (1/3)/ln3^2
Tome dv como 1/x
v = ln x
E só colocar na formula
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por LBT » Seg Nov 01, 2010 13:41
por LBT » Seg Nov 01, 2010 13:41
Maligno escreveu:Ola
Tome u como 1/ln3, pois voce só sabe derivar isso du= (1/3)/ln3^2
Tome dv como 1/x
v = ln x
E só colocar na formula
Estive a ver uma video sobre isto e fiz igual a ti! Agora,
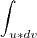
=

-


=
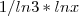
-


=
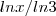
-

aqui temos de fazer

que é a mesma coisa :S
Onde errei?
Pode ficar

??
Obrigado pela tua resposta,
LBT
-
LBT
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Seg Out 18, 2010 16:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Informatica
- Andamento: cursando
 por Neperiano » Seg Nov 01, 2010 16:45
por Neperiano » Seg Nov 01, 2010 16:45
Ola
Cara desculpe estou um pouco sem tempo, mas sei que tem uma regra que da igual no final e no inicio dai tenque passa o da direita pro outro lado tipo
integral xe = xe^2 - integral xe
2integral xe - xe^2/2
Acho que esse caso é assim, qualquer coisa faça mais uma vez por partes
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por LBT » Ter Nov 02, 2010 00:14
por LBT » Ter Nov 02, 2010 00:14
obrigado!
Não estou a conseguir mas amanhã tento de novo!
Cmps
-
LBT
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Seg Out 18, 2010 16:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Informatica
- Andamento: cursando
 por Neperiano » Ter Nov 02, 2010 18:31
por Neperiano » Ter Nov 02, 2010 18:31
Ola
Fiz denovo e cheguei a conclusão que do jeito que estamos fazendo o ln, nunca desaparecera ou seja não dara para integral pois não existe integral dele, com isso há duas possibilidades a primeira escolhemos o u e dv errado e dois é um caso especial de integral e deve fazer que nem eu disse integral até obter dos dois lados a mesma resposta e dai passa pro outro lado, de qualquer forma vou tentar mudar o u e o dv, se conseguir posto aqui
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por LBT » Qua Nov 03, 2010 09:44
por LBT » Qua Nov 03, 2010 09:44
Maligno escreveu:Ola
Fiz denovo e cheguei a conclusão que do jeito que estamos fazendo o ln, nunca desaparecera ou seja não dara para integral pois não existe integral dele, com isso há duas possibilidades a primeira escolhemos o u e dv errado e dois é um caso especial de integral e deve fazer que nem eu disse integral até obter dos dois lados a mesma resposta e dai passa pro outro lado, de qualquer forma vou tentar mudar o u e o dv, se conseguir posto aqui
Atenciosamente
Acho que já sei a solução!
Repare que o

é uma constante, então passei isso para fora e fiz o integral de

!
Penso que seja esta a solução!
Obrigado
-
LBT
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Seg Out 18, 2010 16:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Informatica
- Andamento: cursando
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por andrefahl » Qua Nov 03, 2010 14:26
por andrefahl » Qua Nov 03, 2010 14:26
Qualquer uma que for confirmado a sua sacada foi correta =)
o ln3 é uma CONSTANTE !!! e por "sai" da integral =)
isso é uma propriedade de linearidade da integral,
se for
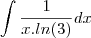
teremos
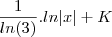
como x eh positivo o modulo nao eh necessário...
se acaso for
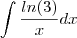
teremos
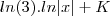
, onde K é a constante arbitraria...
bom essas são as duas primitivas... eu acho =)
AHSDUhASUdhAUSDh
lembrem que

, onde K e C são constantes e F(x) é uma primitiva de f(x)
Espero ter ajudado
-
andrefahl
- Usuário Dedicado

-
- Mensagens: 36
- Registrado em: Qui Out 28, 2010 18:05
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física - UNICAMP
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [INTEGRAL] Integral por partes! Alguem pode me ajudar?
por mih123 » Qua Jan 16, 2013 20:18
- 3 Respostas
- 4584 Exibições
- Última mensagem por adauto martins

Qua Out 22, 2014 09:11
Cálculo: Limites, Derivadas e Integrais
-
- integral por partes
por rita becher » Qua Jun 01, 2011 22:05
- 2 Respostas
- 2313 Exibições
- Última mensagem por rita becher

Qui Jun 02, 2011 10:30
Cálculo: Limites, Derivadas e Integrais
-
- integral por partes
por rita becher » Qui Jun 02, 2011 00:20
- 4 Respostas
- 4003 Exibições
- Última mensagem por rita becher

Sáb Jun 04, 2011 13:01
Cálculo: Limites, Derivadas e Integrais
-
- Integral por Partes
por Guilherme Carvalho » Ter Mar 06, 2012 23:08
- 2 Respostas
- 2106 Exibições
- Última mensagem por Guilherme Carvalho

Qua Mar 07, 2012 10:39
Cálculo: Limites, Derivadas e Integrais
-
- integral por partes
por gasparina nunes » Sáb Abr 07, 2012 23:42
- 3 Respostas
- 2558 Exibições
- Última mensagem por fraol

Dom Abr 08, 2012 22:43
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
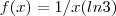 com
com 
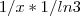
 e
e 
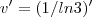 e
e 
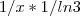 -
- 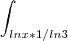 dx, mas como até aqui ja deve estar tudo mal, pois eu não percebi muito bem esta regra, se algue, puder explicar, ficaria muito grato!
dx, mas como até aqui ja deve estar tudo mal, pois eu não percebi muito bem esta regra, se algue, puder explicar, ficaria muito grato! ?
?


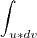 =
=  -
- 
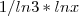 -
-  =
= 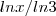 -
- ??
?? é uma constante, então passei isso para fora e fiz o integral de
é uma constante, então passei isso para fora e fiz o integral de  !
!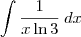



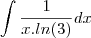 teremos
teremos 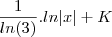 como x eh positivo o modulo nao eh necessário...
como x eh positivo o modulo nao eh necessário...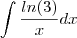 teremos
teremos 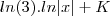 , onde K é a constante arbitraria...
, onde K é a constante arbitraria... , onde K e C são constantes e F(x) é uma primitiva de f(x)
, onde K e C são constantes e F(x) é uma primitiva de f(x)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.