 por Malorientado » Qua Set 19, 2012 22:58
por Malorientado » Qua Set 19, 2012 22:58
(FUVEST-SP) – Uma urna contém 20 bolas numeradas de 1 a 20. Seja o experimento: retirada de
uma bola. Considere os eventos: A = {a bola retirada possui um múltiplo de 2}; B = {a bola retirada
possui um múltiplo de 5}. Então, probabilidade do evento AUB é:
Achei p(A)=11/20, p(B)=1/4 e p(A intersecção B)= 11/80, como p(AUB)=p(A)+p(B)-p(A intersecção B), obtive resolvendo 53/80. Onde errei?
-
Malorientado
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Seg Ago 06, 2012 23:41
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por fraol » Sex Set 21, 2012 22:44
por fraol » Sex Set 21, 2012 22:44
Malorientado escreveu:(FUVEST-SP) – Uma urna contém 20 bolas numeradas de 1 a 20. Seja o experimento: retirada de
uma bola. Considere os eventos: A = {a bola retirada possui um múltiplo de 2}; B = {a bola retirada
possui um múltiplo de 5}. Então, probabilidade do evento AUB é:
Achei p(A)=11/20, p(B)=1/4 e p(A intersecção B)= 11/80, como p(AUB)=p(A)+p(B)-p(A intersecção B), obtive resolvendo 53/80. Onde errei?
Se o evento A é retirar uma bola com número múltiplo de 2 então
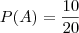
.
Se o evento B é retirar uma bola com número múltiplo de 5 então

.
A interseção entre os eventos A e B são as bolas com os números 10 e 20, ou seja

.
Daí dá para você comparar com a sua solução e concluir o exercício.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por Malorientado » Sex Set 21, 2012 23:02
por Malorientado » Sex Set 21, 2012 23:02
O número 1 também não é um múltiplo?
-
Malorientado
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Seg Ago 06, 2012 23:41
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por fraol » Sex Set 21, 2012 23:06
por fraol » Sex Set 21, 2012 23:06
Os múltiplos de 2, entre 1 e 20, são: 2, 4, 6, 8, 10, 12, 14, 16, 18 e 20.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por Malorientado » Sáb Set 22, 2012 11:41
por Malorientado » Sáb Set 22, 2012 11:41
Amigo me desculpe prolongar esta dúvida mas o número 1 não é um múltiplo de todos? As bolas são numeradas de 1 a 20, há então uma bola 1.
-
Malorientado
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Seg Ago 06, 2012 23:41
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por fraol » Sáb Set 22, 2012 12:34
por fraol » Sáb Set 22, 2012 12:34
Malorientado escreveu:Amigo me desculpe prolongar esta dúvida mas o número 1 não é um múltiplo de todos? As bolas são numeradas de 1 a 20, há então uma bola 1.
Tudo bem. Uma definição de múltiplo é a seguinte:
Um múltiplo de um número é outro número que o contém um número inteiro de vezes. Em outras palavras, um múltiplo de um número

é um número tal que, dividido por

, resulta em um número inteiro.
Conforme essa definição, se 1 fosse múltiplo de 2 então

deveria resultar um número inteiro. Mas isso não acontece, certo?
Outra observação é a de que qualquer número múltiplo de 2 é um número par.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
Voltar para Probabilidade
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [União de 4 Conjuntos]
por ofhell » Qui Mai 03, 2012 13:54
- 1 Respostas
- 4063 Exibições
- Última mensagem por MarceloFantini

Dom Mai 06, 2012 00:02
Conjuntos
-
- União de intervalos.
por eu_dick1 » Sex Mai 23, 2014 14:16
- 4 Respostas
- 3423 Exibições
- Última mensagem por alienante

Sáb Mai 24, 2014 21:09
Conjuntos
-
- União/Interseção de Conjuntos
por joaofonseca » Qui Jan 10, 2013 00:28
- 1 Respostas
- 2607 Exibições
- Última mensagem por fraol

Seg Fev 11, 2013 17:41
Conjuntos
-
- duvida em união interseção de um conjunto
por kzacristo19 » Seg Ago 26, 2013 01:08
- 0 Respostas
- 1509 Exibições
- Última mensagem por kzacristo19

Seg Ago 26, 2013 01:08
Conjuntos
-
- [Problemas] Relação entre união e interseção
por amandasousa_m » Qui Ago 15, 2013 08:59
- 1 Respostas
- 3908 Exibições
- Última mensagem por MateusL

Sex Ago 16, 2013 12:46
Conjuntos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


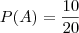 .
. .
. .
.
 é um número tal que, dividido por
é um número tal que, dividido por  deveria resultar um número inteiro. Mas isso não acontece, certo?
deveria resultar um número inteiro. Mas isso não acontece, certo?