Um conjunto formado por p+2 elementos possui 12 subconjuntos a mais do que um conjunto formado por p elementos. Determine p.
Cheguei na equação abaixo mas não consigo resolvê-la:
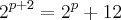

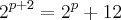

 elementos possui
elementos possui 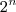 subconjuntos, então:
subconjuntos, então: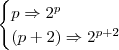
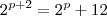
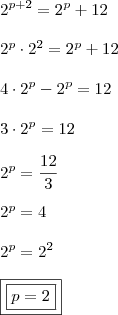

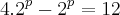 --> Eu pensava que não podia subtrair
--> Eu pensava que não podia subtrair 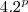 com
com 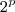 .
. , isso daria
, isso daria 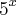 ?
?
Rafael16 escreveu:
Obrigado Daniel !
--> Eu pensava que não podia subtrair com .
No ensino fundamental eu aprendi que primeiro deve resolver as potencias, e só depois resolver as outras operações.
Mas enfim, se tivesse, por exemplo, , isso daria ?
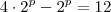
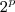 em evidência segue que
em evidência segue que  .
.  natural , temos
natural , temos 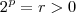 .
. 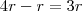 .
.  natural vamos ter um resultado natural multiplo de 3 (
natural vamos ter um resultado natural multiplo de 3 (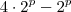 ).
).  , temos
, temos 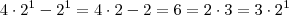 .
.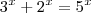 . Para isto ser verdade ,temos que mostrar que para qualquer
. Para isto ser verdade ,temos que mostrar que para qualquer  real a igualdade seja verdadeira .
real a igualdade seja verdadeira .  .
. 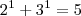 .
. 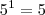 . Parece ser verdadeiro . (Cuidado) Para
. Parece ser verdadeiro . (Cuidado) Para  ,
, 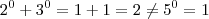 .
. 
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante

 .
.
 :
: