 por Celma » Dom Jul 21, 2013 11:42
por Celma » Dom Jul 21, 2013 11:42
Bom dia!
Eu não entendi a resolução desta inequação.
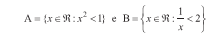
- Inequação.png (1.94 KiB) Exibido 3863 vezes
Obrigada!
-
Celma
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Sex Jun 28, 2013 12:44
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em matemática
- Andamento: cursando
 por MateusL » Dom Jul 21, 2013 16:27
por MateusL » Dom Jul 21, 2013 16:27
Celma, coloque o enunciado da questão.
Abraço!
-
MateusL
- Usuário Parceiro

-
- Mensagens: 68
- Registrado em: Qua Jul 17, 2013 23:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Celma » Dom Jul 21, 2013 18:40
por Celma » Dom Jul 21, 2013 18:40
Dado os conjuntos A e B.
As alternativas tem intervalos como resposta. Eu nao consegui anexar porque excedeu o tamanho do arquivo
-
Celma
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Sex Jun 28, 2013 12:44
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em matemática
- Andamento: cursando
 por MateusL » Dom Jul 21, 2013 19:47
por MateusL » Dom Jul 21, 2013 19:47
Mas o exercício pede para encontrar o intervalo que representa o que? A intersecção desses dois conjuntos? A união desses dois conjuntos?
Abraço
-
MateusL
- Usuário Parceiro

-
- Mensagens: 68
- Registrado em: Qua Jul 17, 2013 23:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Celma » Dom Jul 21, 2013 20:54
por Celma » Dom Jul 21, 2013 20:54
Oi Mateus, vou recomeçar.
O enunciado diz apenas: Dados os conjuntos

- Inequação.jpg (7.24 KiB) Exibido 3834 vezes
pode se afirmar que:
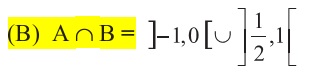
- resposta.jpg (6.99 KiB) Exibido 3834 vezes
Não é possível anexar todas as opções porque acaba excedendo o tamanho do arquivo, então coloquei apenas a resposta correta.
Ocorre que não consigo chegar neste intervalo e gostaria de ver desenvolvido para entender onde estou errando.
Obrigada
-
Celma
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Sex Jun 28, 2013 12:44
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em matemática
- Andamento: cursando
 por MateusL » Dom Jul 21, 2013 22:23
por MateusL » Dom Jul 21, 2013 22:23
Analisando o conjunto

:
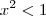
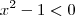
Achando as raízes por bháskara e analisando a concavidade da parábola (neste caso, concavidade voltada para cima, pois o coeficiente de

é positivo).


Ou seja,
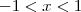
. Então:
![A=]-1,1[ A=]-1,1[](/latexrender/pictures/dd38bc8922055cbcbbaee33e2e409b8e.png)
Analisando o conjunto B:

Se

:

Então temos

e

, implicando que

.
Se
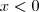
:

Então temos
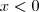
e

, implicando que
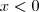
.
Então:
![B=]-\infty,0[\cup\left]\dfrac{1}{2},+\infty\right[ B=]-\infty,0[\cup\left]\dfrac{1}{2},+\infty\right[](/latexrender/pictures/451a0ba16c3ad8391cbc2272a7dee08a.png)
Resumindo:
![A=]-1,1[ A=]-1,1[](/latexrender/pictures/dd38bc8922055cbcbbaee33e2e409b8e.png)
![B=]-\infty,0[\cup\left]\dfrac{1}{2},+\infty\right[ B=]-\infty,0[\cup\left]\dfrac{1}{2},+\infty\right[](/latexrender/pictures/451a0ba16c3ad8391cbc2272a7dee08a.png)
Agora é só fazer as operações com esses intervalos.
Abraço!
-
MateusL
- Usuário Parceiro

-
- Mensagens: 68
- Registrado em: Qua Jul 17, 2013 23:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Inequações
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.







 :
: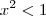
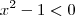
 é positivo).
é positivo).

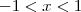 . Então:
. Então:![A=]-1,1[ A=]-1,1[](/latexrender/pictures/dd38bc8922055cbcbbaee33e2e409b8e.png)

 :
:
 e
e  , implicando que
, implicando que  .
.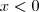 :
:
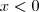 e
e  , implicando que
, implicando que 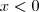 .
.![B=]-\infty,0[\cup\left]\dfrac{1}{2},+\infty\right[ B=]-\infty,0[\cup\left]\dfrac{1}{2},+\infty\right[](/latexrender/pictures/451a0ba16c3ad8391cbc2272a7dee08a.png)
![A=]-1,1[ A=]-1,1[](/latexrender/pictures/dd38bc8922055cbcbbaee33e2e409b8e.png)
![B=]-\infty,0[\cup\left]\dfrac{1}{2},+\infty\right[ B=]-\infty,0[\cup\left]\dfrac{1}{2},+\infty\right[](/latexrender/pictures/451a0ba16c3ad8391cbc2272a7dee08a.png)





 , avisa que eu resolvo.
, avisa que eu resolvo.

