Percebi, ao resolver eu havia posto P= 2x+y, porque ja existia uma parede, e nao tomei em conta o 4, sim ja resolvi, teremos que A=x(100-2x)= -2x²+100x, se querem as dimensoes querem o valor de comprimento(x) e a largura(y), entao se queremos o comprimento(x-xv) Xv= -b/2a, entao teremoss x=100/4=25, apartir daí ja podemos calcular o valor da largura(y), apos termos feito no perimetro inscrito, isto é: 4(2x+y)=400; 8x+4y, y=400-8x/4= 100-2x, entao partir daí temos que y=100-2x, entao: 100-2.25= 50; Conclusao: o lado oposto á parede medirá 50m e os seus adjacentes mediram cada um 25m. Jedi eu te agradeço bastante...!!! Muito obrigadoo, obrigado mesmo! Óptimo dia! Mais uma vez Obrigado







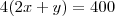





 .
.



