 por R0nny » Sáb Mai 04, 2013 15:01
por R0nny » Sáb Mai 04, 2013 15:01
Um fazendeiro quer construir um curral rectangular. Para cercá-lo, dispoe de 400 m de arame e de uma parede já existente. Sabendo que a cerca de arame terá 4 voltas, determine as dimensoes desse curral para que a sua área seja máxima. Fonte: Questao foi colocado por meu Professor(Adolfo Magode). Entao, neste exercicio temos que ter em conta duas condiçoes o perimetro do rectangulo e a área do rectangulo, eu calculei usando o perimetro= 4x+4y=400, pois o problema diz que o arame( a parte externa do curral) dá 4 voltas, sabendo que o perimetro de um rectangulo é dado por: P= 2x+2y, no final obtive 50m por 200m, mas o gabarito deste exercicio diz que é 25m por 50m.

-
R0nny
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Dom Abr 28, 2013 10:53
- Formação Escolar: ENSINO FUNDAMENTAL II
- Área/Curso: Estudante
- Andamento: cursando
 por young_jedi » Sáb Mai 04, 2013 18:44
por young_jedi » Sáb Mai 04, 2013 18:44
o enunciado diz que já existe uma parede que ira formar o retângulo
portanto você terá que cercar dois lados x e um lado y portanto você tem que
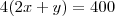
tente concluir e comente se tiver duvidas
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por R0nny » Sáb Mai 04, 2013 19:51
por R0nny » Sáb Mai 04, 2013 19:51
Percebi, ao resolver eu havia posto P= 2x+y, porque ja existia uma parede, e nao tomei em conta o 4, sim ja resolvi, teremos que A=x(100-2x)= -2x²+100x, se querem as dimensoes querem o valor de comprimento(x) e a largura(y), entao se queremos o comprimento(x-xv) Xv= -b/2a, entao teremoss x=100/4=25, apartir daí ja podemos calcular o valor da largura(y), apos termos feito no perimetro inscrito, isto é: 4(2x+y)=400; 8x+4y, y=400-8x/4= 100-2x, entao partir daí temos que y=100-2x, entao: 100-2.25= 50; Conclusao: o lado oposto á parede medirá 50m e os seus adjacentes mediram cada um 25m. Jedi eu te agradeço bastante...!!! Muito obrigadoo, obrigado mesmo! Óptimo dia! Mais uma vez Obrigado


-
R0nny
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Dom Abr 28, 2013 10:53
- Formação Escolar: ENSINO FUNDAMENTAL II
- Área/Curso: Estudante
- Andamento: cursando
Voltar para Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- problemas com equacoes de 1 grau
por luanxd » Qua Jan 27, 2010 23:14
- 2 Respostas
- 2339 Exibições
- Última mensagem por luanxd

Sáb Jan 30, 2010 23:31
Polinômios
-
- Problemas com equações biquadradas
por Viivii » Qua Ago 24, 2011 23:05
- 4 Respostas
- 4037 Exibições
- Última mensagem por Neperiano

Qui Ago 25, 2011 17:59
Sistemas de Equações
-
- Problemas matemáticos envolvendo equações.
por mynameisnandoo » Qui Out 06, 2011 14:57
- 0 Respostas
- 2650 Exibições
- Última mensagem por mynameisnandoo

Qui Out 06, 2011 14:57
Tópicos sem Interação (leia as regras)
-
- Problemas com equações do 2° Questão valendo 1 ponto
por jvpetrucci » Qui Mai 03, 2012 19:14
- 12 Respostas
- 6164 Exibições
- Última mensagem por Russman

Qui Mai 03, 2012 22:35
Sistemas de Equações
-
- [Problemas de Valor Inicial] Equações Diferenciais
por mayconf » Ter Abr 15, 2014 18:24
- 1 Respostas
- 2113 Exibições
- Última mensagem por Russman

Ter Abr 15, 2014 22:28
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.











 , avisa que eu resolvo.
, avisa que eu resolvo.

