 por PedroCunha » Dom Set 23, 2012 11:46
por PedroCunha » Dom Set 23, 2012 11:46
Olá, sou novo aqui no Fórum e tenho uma questão da CEFET-PR que encontrei em uma prova que fiz e que não consigo resolver. Gostaria de pedir a ajuda de vocês.
--------------------------------------------------------------------------------------------------------------------------
Os valores de p e q para que i seja raiz da equação 2x³ +px² + qx + 2 = 0, são respectivamente: |
|
a. 2 e 2
b. -1e 0
c. 1 e -1
d. 1/2 e 2
e. 1/2 e 0
---------------------------------------------------------------------------------------------------------------------------
Pensei em colocar o x em evidência e resolver a equação do segundo grau que aparece, mas não da certo. Também tentei usar as relações de Girard.
-
PedroCunha
- Usuário Ativo

-
- Mensagens: 21
- Registrado em: Dom Set 23, 2012 11:29
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MarceloFantini » Dom Set 23, 2012 13:35
por MarceloFantini » Dom Set 23, 2012 13:35
Lembre-se que se

é raíz, então

é raíz também. Substitua ambas e resolva o sistema.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por PedroCunha » Dom Set 23, 2012 13:41
por PedroCunha » Dom Set 23, 2012 13:41
Tentei substituir mas não consegui.
Poderia mostrar como faço?
E gostaria de saber se existe outro jeito de responder, pois ainda não vi equações de terceiro grau, logo penso que tenha algum jeito de resolver esse exercício com equações de segundo grau ou algo do tipo.
-
PedroCunha
- Usuário Ativo

-
- Mensagens: 21
- Registrado em: Dom Set 23, 2012 11:29
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MarceloFantini » Dom Set 23, 2012 13:47
por MarceloFantini » Dom Set 23, 2012 13:47
Substituindo a primeira:

.
Substituindo a segunda:

.
Agora somando as duas temos

e

. Substitua de volta em alguma delas e encontre

.
O único fato que você precisava saber é que raízes complexas aparecem aos pares: se um número complexo é raíz, seu conjugado também é.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por PedroCunha » Dom Set 23, 2012 13:50
por PedroCunha » Dom Set 23, 2012 13:50
Entendi. Muito obrigado.
Só uma coisa. Sendo uma equação do terceiro grau, ela não deveria ter três raízes?
-
PedroCunha
- Usuário Ativo

-
- Mensagens: 21
- Registrado em: Dom Set 23, 2012 11:29
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MarceloFantini » Dom Set 23, 2012 13:52
por MarceloFantini » Dom Set 23, 2012 13:52
Ela tem mais uma raíz real, mas não é necessário saber qual é.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por PedroCunha » Dom Set 23, 2012 13:53
por PedroCunha » Dom Set 23, 2012 13:53
Ok.
Teria algum jeito de fazer essa questão colocando o "x" em evidência?
-
PedroCunha
- Usuário Ativo

-
- Mensagens: 21
- Registrado em: Dom Set 23, 2012 11:29
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MarceloFantini » Dom Set 23, 2012 14:00
por MarceloFantini » Dom Set 23, 2012 14:00
Não, pois zero não é raíz. Além de tudo, para fatorar e encontrar

e

de outra forma você já deveria conhecer todas as raízes, e não dá pra saber qual é a outra raíz real sem saber os coeficientes.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por PedroCunha » Dom Set 23, 2012 14:01
por PedroCunha » Dom Set 23, 2012 14:01
Ok. Obrigado. Acho que meu professor errou a mão então, pois ele não havia explicado que quando i é raiz, seu conjugado também é.
-
PedroCunha
- Usuário Ativo

-
- Mensagens: 21
- Registrado em: Dom Set 23, 2012 11:29
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por PedroCunha » Dom Nov 11, 2012 11:17
por PedroCunha » Dom Nov 11, 2012 11:17
Nessa questão, quando chego em:
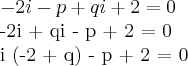
Posso falar que
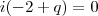
é a parte imaginária e que
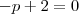
é a parte real e igualar as duas a zero e depois achar os valores de p e q, da seguinte forma?

Att.,
Pedro
-
PedroCunha
- Usuário Ativo

-
- Mensagens: 21
- Registrado em: Dom Set 23, 2012 11:29
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MrJuniorFerr » Dom Nov 11, 2012 12:26
por MrJuniorFerr » Dom Nov 11, 2012 12:26
Eu nunca estudei números complexos, mas eu não quero ficar com uma dúvida...
Marcelo, como você fez isso?
MarceloFantini escreveu:Substituindo a primeira:

Substituindo a segunda:

.
Não entendi como foi feito as substituições,os expoentes sumiram.
-

MrJuniorFerr
- Colaborador Voluntário

-
- Mensagens: 119
- Registrado em: Qui Set 20, 2012 16:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Alimentos
- Andamento: cursando
 por PedroCunha » Dom Nov 11, 2012 12:34
por PedroCunha » Dom Nov 11, 2012 12:34
O que ele fez foi usar as propriedades dos número complexos.

-
PedroCunha
- Usuário Ativo

-
- Mensagens: 21
- Registrado em: Dom Set 23, 2012 11:29
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por PedroCunha » Seg Nov 12, 2012 19:18
por PedroCunha » Seg Nov 12, 2012 19:18
Alguém?
-
PedroCunha
- Usuário Ativo

-
- Mensagens: 21
- Registrado em: Dom Set 23, 2012 11:29
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MarceloFantini » Seg Nov 12, 2012 19:22
por MarceloFantini » Seg Nov 12, 2012 19:22
Pedro, acredito que pode sim. Havia me esquecido desta possibilidade.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por PedroCunha » Seg Nov 12, 2012 20:43
por PedroCunha » Seg Nov 12, 2012 20:43
Que ótimo,

! Facilita muito.
Obrigado Marcelo.
-
PedroCunha
- Usuário Ativo

-
- Mensagens: 21
- Registrado em: Dom Set 23, 2012 11:29
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Questão 27 do CEFET MG 2007
 por Eduardo Goncalves » Sex Fev 10, 2012 10:41
por Eduardo Goncalves » Sex Fev 10, 2012 10:41
- 5 Respostas
- 7783 Exibições
- Última mensagem por LuizAquino

Sáb Fev 11, 2012 12:52
Geometria Plana
-
- Questão CEFET-MG 2012
por Thulio_Parazi » Qui Abr 05, 2012 13:48
- 5 Respostas
- 4824 Exibições
- Última mensagem por fraol

Ter Abr 10, 2012 20:02
Trigonometria
-
- Cefet-mg 2012 questão 03
por Thulio_Parazi » Sex Abr 13, 2012 11:12
- 4 Respostas
- 4490 Exibições
- Última mensagem por fraol

Qua Abr 18, 2012 22:26
Logaritmos
-
- [questao do cefet mg matemática]
por tayna01 » Ter Abr 22, 2014 12:13
- 1 Respostas
- 2714 Exibições
- Última mensagem por adauto martins

Seg Jan 05, 2015 14:52
Números Complexos
-
- Questão CEFET-MG graduação 2012
por Thulio_Parazi » Qui Abr 05, 2012 11:24
- 1 Respostas
- 2133 Exibições
- Última mensagem por fraol

Sex Abr 06, 2012 20:54
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 é raíz, então
é raíz, então  é raíz também. Substitua ambas e resolva o sistema.
é raíz também. Substitua ambas e resolva o sistema.


 .
. .
. e
e  . Substitua de volta em alguma delas e encontre
. Substitua de volta em alguma delas e encontre  .
.





 e
e  de outra forma você já deveria conhecer todas as raízes, e não dá pra saber qual é a outra raíz real sem saber os coeficientes.
de outra forma você já deveria conhecer todas as raízes, e não dá pra saber qual é a outra raíz real sem saber os coeficientes.


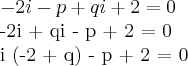
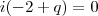
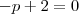


.






 ! Facilita muito.
! Facilita muito.





